高一年级第一学期期中数学卷
一、选择题(本大题共10小题,每小题5分,共50分)
1、在(0,+∞)上为增函数的是:( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、下列运算正确的是:( )
A、若![]() ,则
,则![]() B、若
B、若![]() ,则
,则![]()
C、若![]() ,则
,则![]() D、
D、![]()
3、![]()
![]() 的反函数为:(
)
的反函数为:(
)
A、y=2x-3 (x<2)
B、![]() (x≥2)
(x≥2)
C、![]() (x≥1)
D、y=3-2x (x<2)
(x≥1)
D、y=3-2x (x<2)
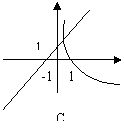
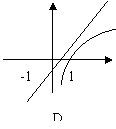
4、![]() 的图象可能是:(
)
的图象可能是:(
)
![]()


|
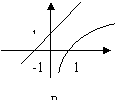
| |||
5、![]() 在第一象限为增函数,则m的取值范围是:( )
在第一象限为增函数,则m的取值范围是:( )
A、m<-2或m>1 B、m∈R
C、-2<m<1 D、m>2或m<-1
6、若![]() ,
,![]() ,
,![]() 则(
)
则(
)
A、a<b<c B、c<a<b C、b<a<c D、a<c<b
7、如果函数![]() 值域为[-2,5],则其定义域为( )
值域为[-2,5],则其定义域为( )
A、[-2,2] B、[-1,1]
C、![]() D、
D、![]()
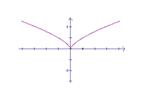
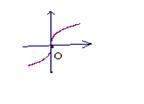
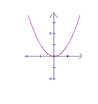
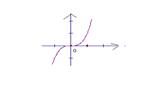 8、
8、![]() 的大致图象为:(
的大致图象为:(
A B C D
9、![]() 则a的取值范围为:( )
则a的取值范围为:( )
A、{a1<a<3} B、{a2<a<3或a>3或a<-1}
C、{a1<a<3或a>3或a<-1} D、{aa<-1}
10、已知![]() 的值域为
的值域为![]() ,定义域为A,当x∈A时,
,定义域为A,当x∈A时,
![]() 的值域为:( )
的值域为:( )
A、[-1,0) B、[-1,0] C、[0,1) D、(0,1]
二、填空题(本大题共4小题,每小题5分,共20分)
11、已知A={x,xy,lg(xy) },B={0,x },若![]() ,
,
则x= ,y=
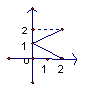
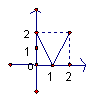 12、设集合M={x0≤x≤2},N={y0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有
12、设集合M={x0≤x≤2},N={y0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有
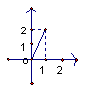
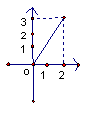
① ② ③ ④
13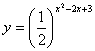 的减区间为
。
的减区间为
。
14、f(x)为R上的奇函数,且为增函数,则![]() 的解集为{x
}
的解集为{x
}
三、解答题(本大题共6小题,共54分.解答应写出文字说明,证明过程或演算步骤.):
15.(本小题满分12分)计算:
(1)![]() (2)
(2)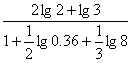
16.(本小题满分12分)解方程:
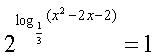
17.(本小题满分12分)
用定义证明![]() 在定义域上是单调减函数。
在定义域上是单调减函数。
18.(本小题12分)
已知 ![]()
(1)求f(x)的定义域,并解f(x)>0;
(2)判定f(x)的奇偶性,并给出证明。
19.(本小题满分16分)
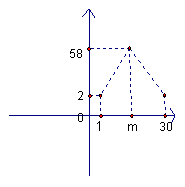 在6月份(30天)某服装上市,日销量(单位:件)f(x)关于时间x的函数关系如图:
在6月份(30天)某服装上市,日销量(单位:件)f(x)关于时间x的函数关系如图:
![]()
价格为![]() (单位:元),
(单位:元),
(1)求a,b,写出f(x)的表达式。
(2)求日收入最好的一天的销售额。
20、(本小题满分16分)
若![]() ,如果G(x)的零点(即G(x)的图象与x轴交点的横坐标)分别在区间(-1,0)和(2,3)内,
,如果G(x)的零点(即G(x)的图象与x轴交点的横坐标)分别在区间(-1,0)和(2,3)内,
(1)作出G(x)的简图;
(2)求m的取值范围。