高一年级数学上学期期中考试试题
（满分：100分，时间：90分钟） 2006.11.13
一、填空题（每题4分，共40分）
1．集合
用列举法表示为 ；
2．函数
的定义域是 ；
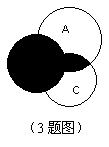
3．右图中的阴影部分用集合表示为 ；
4．若关于
的不等式
的解集是 (1，4 )，则
；
5．命题“若
”的逆命题是 ；
6．设集合
；
7．不等式
的解为 ；
8．已知集合
，若
，则实数
＝ ；
9．命题甲：集合
为空集；命题乙：关于的不等式
的解集为
．若命题甲、乙中有且只有一个是真命题，则实数
的取值范围是 ；
10．定义
的“长度”．已知集合
，
，那么集合
的“长度”是 ．
二、选择题（每题4分，共16分）
11．命题“
”是命题“
”的（ ）条件
A．充分非必要 B．必要非充分 C．充要 D．非充分非必要
12．给出下列命题：
（1）若集合
的交集是空集，则中至少有一个是空集
（2）对于实数
（3）设为任意实数，则
的最小值为4
（4）函数
与函数
是同一函数
其中真命题的个数是（ ）
A．0个 B．1个 C．2个 D．3个
13．某个命题与自然数
有关．如果当
时该命题成立，那么可推得当
时该命题也成立．现已知当
时该命题不成立，那么可推得( )
A．当
时该命题不成立
B．当时该命题成立
C．当
时该命题不成立
D．当时该命题成立
14．设
的解集是（ ）
A．[2，3] B．[2，4] C．
D．
三、解答题（共44分）
15．（8分）设全集
,
,
，求的值．
16．（8分）解关于的不等式
．
17．（10分）已知集合
（1）求集合
；
（2）当
的取值范围．
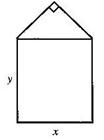18．（10分）某单位用木料制作如图所示的框架，框架的下部是边长分别为
(单位：
)的矩形，上部是等腰直角三角形，要求框架围成的总面积8
．
（1）试用表示
，并求出的取值范围；
（2）问为多少(精确到0.001) 时用料最省？
19．（8分）设非空集合
具有如下性质：①元素都是正整数；②若
．
（1）请你写出符合条件,且分别含有一个、二个、三个元素的集合各一个；（3分）
（2）是否存在恰有6个元素的集合？若存在，写出所有的集合；若不存在，请说明理由；（2分）
（3）由(1)、(2)的解答过程启发我们，可以得出哪些关于集合的一般性结论（要求至少写出两个结论）？（3分）
高一年级数学期中考试试题（答题纸）
（满分：100分，时间：90分钟） 2006.11.13
一、填空：
1． ；2． ；3． ；4． ；
5． ；6． ；
7． ；8． ；9． ；10． 。
二、选择：
11． 12． 13． 14．
三、解答：
15．
16．
17．
18．
19．
高一年级数学期中考试试题答案
一 填空题
1. 
2. 
3. 
4. –1 5. 若
则
6. 
7. 
8. –1
9. 
10. 
二 选择题
11. B 12. A 13. C 14. C
三 解答题
15 由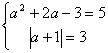
得 
16. 原不等式可变形为：
当
当
， 
当
当
17. (1) A=(-1,3)
(2) 由题意得：B: （x-3a）(x-a) < 0
1)当a=0时
B= 满足题意
2)当a>0时， B=(a,3a) 要使
则
3)当a<0时， B=(3a,a) 要使 则
综上：
18. (1) 由框架总面积为8 
得：
由
得 
（2） 用料L = 
=
=
当且仅当：
即 
时 取到等号。
当
时，用料最省。
19． （1）一元：
二元：
等 三元：
等
（2） 存在。 一共有四个
S= 
或S= 
或S= 
或S= 
(3)
例如：① 
；
② 若
则s中的元素个数为奇数个，
若 
则s中的元素个数为偶数个；
③ 符合题意的S共有31个。 等等