高一上学期期末考试数学模拟题
总分150分
一选择题(共50分)
1、设全集U={1,2,3,4,5},集合M={1,2,3},N={2,3,5},则![]() =
=
(A)Φ (B) {2,3} (C) {4} (D) {1,5}
2设x∈R,则 x﹣2 <3是0<x<5的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分且不必要条件
3已知a>0,且a≠1,则下述结论正确的是
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
4已知函数f(x)满足f(x)=x3+2,则![]() 等于
等于
(A) ![]() (B) -1 (C)
(B) -1 (C) ![]() (D) 3
(D) 3
5计算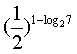 的值为
的值为
(A) 14
(B) ![]() (C)
6
(D)
(C)
6
(D) ![]()
6当![]() 时,在同一坐标系中,函数
时,在同一坐标系中,函数![]() 与
与![]() 的图象是
的图象是
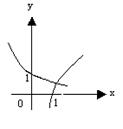
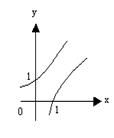
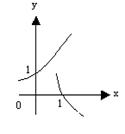
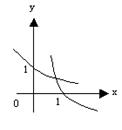
(A) (B) (C) (D)
7.已知映射f: A→B,其中集合A={﹣3,﹣2,﹣1, 1, 2, 3, 4},集合B中的元素都是A中元素映射f下的像,且对任意的a∈A,在B中与它对应的元素是a, 则集合B是
A.{﹣3,﹣2, -1, 1, 2, 3, 4 } B.{1, 2, 3 } C.{1, 2, 3, 4 } D.{﹣1,﹣2,﹣3 }
8.设p, q是两个简单命题,下列命题中正确的是
A. P和非P可能同时成立
B.若p, q中只有一个真命题,则“p且q”为真命题
C.若p,q都为假命题,则“p或q”有可能为真命题
D.若p, q中只有一个真命题,则“p或q”为真命题
9函数f(x)=![]() (6﹣x﹣x2)的单调递增区间是
(6﹣x﹣x2)的单调递增区间是
A.![]() B.
B.![]() C.
C.![]() D.(﹣3,
D.(﹣3, ![]()
10、等比数列![]() 中,已知
中,已知![]() ,
,![]() 则
则![]() =
=
(A)91 (B)49 (C)105 (D)112
二 填空题(共20分)
11函数y=lg(9-x2)的定义域 。 12 命题“若x 2+y 2=0,则x、y全为0”的否命题是
13.在数列{an}中,首项a1=1,an=2an-1+1(n≥2,n∈N),则a4=______________。
14.已知f(x)= 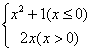 若f(x)=10,则x=________________________。
若f(x)=10,则x=________________________。
15、已知等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() 等于
等于
三 解答题(共80分)
16 (满分12分)成等差数列的三个正数的和等于15,并且这三个数分别加上1,3,9后又成等比数列,求这三个数。
17、(本题满分12分)
已知函数![]()
(1)求函数f(x)的反函数![]() ;
;
(2)用单调性的定义证明:![]() 在(2,+∞)上是减函数。
在(2,+∞)上是减函数。
18(本小题满分14分)
已知函数f(x)=ax2+(a+2)x+b.
(1)若a=0,当﹣1<x<1时,f(x)>0恒成立,求实数b的取值范围;
(2)若f(0)= ![]() ,当x∈R时f(x)≥0恒成立,求函数f(a)=(a﹣4)(1+a﹣1)的值域.
,当x∈R时f(x)≥0恒成立,求函数f(a)=(a﹣4)(1+a﹣1)的值域.
19(本题满分14分)
已知数列{a n}满足 a 1=1,以后各项由公式![]() 给出,
给出,
(1) 写出这个数列的前4项;
(2)
若![]() ,求证:数列{b n}是等比数列;
,求证:数列{b n}是等比数列;
(3) 求数列{a n}的通项公式;
(4) 求数列{a n}的前n项和S n 。
20(本题满分14分)集合A是由适合以下性质的函数f(x)组成的,对于任意的x≥0,f(x)∈![]() 且f(x)在(0,+∞)上是增函数.
且f(x)在(0,+∞)上是增函数.
(1)试判断f1(x)= ![]() 及f2(x)=4﹣6(
及f2(x)=4﹣6(![]() )x (x≥0)是否在集合A中,若不在集合A中,试说明理由;
)x (x≥0)是否在集合A中,若不在集合A中,试说明理由;
(2)对于(1)中你认为是集合A中的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意x≥0总成立?试证明你的结论.
21(本题满分14分)已知数列{an}中,a1=1, a2n+1+an2+1
=2(an+1an+an+1﹣an),求数列![]() 的前n项和Sn.
的前n项和Sn.
高一上学期期末考试数学模拟题模拟题答案

| 题号 | 一 | 二 | 三 | 总分 | |||||
| 18 | 19 | 20 | 21 | 22 | 23 | ||||
| 得分 | |||||||||
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | C | B | D | B | B |
| 题号 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | D | B | A |
二填空题
11(-3,3) 12 、若x 2+y 2≠0,则x、y不全为0
13 15 14 -3或5
15 72
三解答题
16解: 设所求的三个数为a-d,a,a+d ……3分
则由题可知:a-d+a+a+d=3a=15 Þ a=5 ……6分
于是由5-d+1,5+3,5+d+9成等比数列
Þ(6-d)(14+d)=64 Þ d 2+8d-20=0 Þ d=2或d=-10 ……10分
代入得所求三个数为3,5,7或15,5,-5(舍去) ……6分
17解: (1)由函数![]() 得
得![]() ,
,
所以该函数的反函数是![]() ……5分
……5分
(2)在(2,+∞)上任取![]() ,设
,设![]() ……6分
……6分
则![]() ……8分
……8分
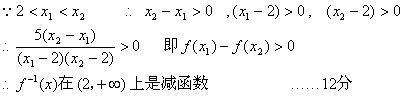
18(1)![]() 时
时 ![]()
当![]() 时
时 ![]() 恒成立
恒成立
![]() 则
则![]()
![]() ……………3分
……………3分
![]()
得![]()
![]()
![]()
解得![]() ……………5分
……………5分
(2)若![]()
![]() ……………6分
……………6分
当![]() 时
时![]() 不可能恒成立
不可能恒成立![]()
![]() 当
当![]() 时要使
时要使![]() 恒成立,则
恒成立,则 ![]()
![]() ……………8分
……………8分
解得:![]() ……………1分
……………1分
![]() ……………10分
……………10分
当![]() 时
时![]()
当![]()
![]() 值域
值域![]() ……………14分
……………14分
19解:(1)a1=1,a2=![]() ,a3=
,a3=![]() ,a4=
,a4=![]() ……3分
……3分
(2) ![]() 整理得
整理得
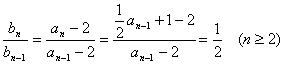 是常数
是常数
所以数列{b n}是以-1为首项,![]() 为公比的等比数列 ……7分
为公比的等比数列 ……7分
(3) ![]() …… 10分
…… 10分
(4)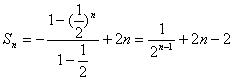 ……14分
……14分
20(1)![]()
![]()
![]() 不在集合A中
……………3分
不在集合A中
……………3分
又![]() 的值域
的值域![]() ,
,![]()
当![]() 时
时![]() 为增函数(要证明)
为增函数(要证明)
![]() 在集合A中
……………7分
在集合A中
……………7分
(2)![]()
![]()
![]()
![]() 对任意
对任意![]() ,不等式
,不等式![]() 总成立 …14分
总成立 …14分
21 ![]()
![]()
![]()
![]()
![]()
![]() 为等差数列
为等差数列
![]() …………8分
…………8分
![]()
![]()
=![]()
=![]()
![]()
![]()