高一数学下综合测试（二）

高一数学下综合测试（二）

一．选择题（每小题5分，共60分）

1．α为第二象限角，P(x, )为其终边上一点，且cosα＝x，则x值为(　　)

　A．　　　　　　　　　　　B．±　　　　　　　　　　　C．－　　　　　　　　　D．－

2．曲线的一条对称轴是（　）

A. 　　　 B.　　　　C.　　　　D.

3．如果1弧度的圆心角所对的弦长为2，则这个圆心角所对的弧长为(　　)　

　A．　　　　　　　　　B．sin0.5　　　　　　　　　　 C．2sin0.5　　　　　　　　D．tan0.5

4 ．下列命题中正确的是 （　　　）

（A）　　　　　 （B）　 　　　　

（C）　　　　（D）

5．下列坐标所表示的点不是函数的图象的对称中心的是

　　（A）（，0）　 （B）（，0）　 （C）（，0） 　（D）（，0）

6．已知

　 A．　　　　　 B．　　　　 C．　　　　D．

7．给出下列三个向量等式：（1）（2）（3） ，其中正确的等式的个数为（　　 ）

（A）0　　　　　 （B）1　 　　　　（C）2 　　　　 （D）3

8．以下给出的函数中，以为周期的偶函数是（　）

　 　　　　　

9．集合与的关系为（　 ）

AB　　(B) AB　　　　

10．已知sinα＞sinβ，则下列命题成立的是(　　)

A．若α.β是第一象限角，则cosα＞cosβ．B．若α.β是第二象限角，则tanα＞tanβ．

C．若α.β是第三象限角，则cosα＞cosβ．D．若α.β是第四象限角，则tanα＞tanβ

11．将函数的图象上每点的横坐标缩小为原来的（纵坐标不变），再把所得图象向左平移个单位，得到的函数解析式为（　 ）

　　 　

12．使（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为（　　　）

A．　 　　　　　 B．　　　　　 C．π　　　　　　　　　 D．

二、填空题（每小题4分，共16分）

13．为锐角，　　　　　　　　

14．单调增区间为　　　　　　

15．的定义域为

16．下列命题中正确的序号为（你认为正确的都写出来）

①的周期为，最大值为；

②若x是第一象限的角，则是增函数；

③在中若则；

④既不是奇函数，也不是偶函数；

⑤且．

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

13、　　　　　　　　　　　　　　　  ，14、　　　　　　　　　　　　　　　 

15、　　　　　　　　　　　　　　 　 ，16、　　　　　　　　　　　　　　　 

三．解答题（共74分）

17．（本小题12分）（1）化简：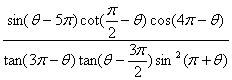

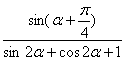 (2)已知为第二象限的角，且,求的值。

18．（本小题12分）已知函数,（1）求函数的最小正周期和最大值，并求出取得最大值时的集合；（2）在给出的直角坐标系中，画出函数在区间上的图像。

19．（本小题12分）函数的图像最高点的坐标为（2，），由这个最高点到其相邻的最低点间，图像于X轴相交于点（6，0），求函数的表达式，并指出其振幅、频率、初相。

20．（本小题12分）设, 求证：

21．（本小题12分）在,且A<B<C,求cosA。

22．（本小题14分）若恒成立，求实数m的取值范围。

高一下综合测试（二）答案

一、选择题

CBADD， DCABD， BA

二、填空题

（13）arctan；(14)［kπ—, kπ—］，k∈Z；

(15)［kπ+, kπ+］，k∈Z； （16）①③④⑤

三、解答题

17、①解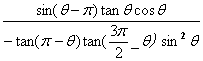： === —1

②由sin=得cosα= —

∴原式=== —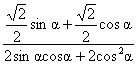

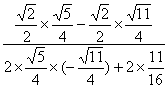18、解：f(x)=3cosx sinx —3cos²x+2=sin2x —cos2x+=3sin(2x-)+

 最小正周期T==π当2x —=+2kπ即x=kπ+，k∈z时f_max=　， x的集合

19、函数表达式为y=sin(x+)，振幅A=，频率为，初相为。

20、证明： 由2sin(+ α)=sinθ+cosθsinα+cosα= sinθ+cosθ

2+4sinαcosα=1+sin2θ　 ①　　 2sin²β=sin2θ　　　　 ②

②代入①得：2+2sin2α=1+2sin²β2sin2α=2sin²β-12sin2α=-cos2β

sin2α+β=0

21、解：∵B=π—（A+C）∴sinB=sin[π—（A+C）]= sin(A+C)=

A<B<C, 0<B<　　 ∴<A+C<π, ∴cos(A+C)= -

0<2A+C<A+B+C=π　　∴sin(2A+C)=

cosA=cos[(2A+C)—(A+C)]= -×(-)+×=

22、解法一：由题cos²θ-2<2m-2msinθ即：cos²θ-2<2m(1-sinθ)　θ∈R恒成立

当sinθ=1时 cos²θ-2<0　恒成立；当sinθ≠1时　　1-sinθ>0

∴2m>　　  设y=　　  令1-sinθ=t

　y== = = -（t+）+2

又t=1-sinθ∈[0,2]　  当t=时，（t+）min=2　　 y_max=-2+2

∴2m>2-2　　∴当m>1-原不等式恒成立

22、解法二：由题意得：sin²θ-2msinθ+2m+1>0对θ∈R恒成立

令t=sinθ　∴t∈[-1,1]

令g（t）=t²-2mt+2m+1=(t-m)²+m²+2m+1,t∈[-1,1]

若m<-1，要g(t)>0恒成立，则一定有g(-1)>0，

无解

即

m<-1

g(-1)>0

 若-1≤m≤1，要使g(t)>0恒成立，则一定有g(m )>0，

1-<m≤1

即

-1≤m≤1

g(m)>0

若m>1，要使g(t)>0恒成立，则一定有g(1 )>0，

m>1

即

m>1

g(1)>0

综上所述：当m>1-时，对θ∈R时，原不等式恒成立