高一数学下综合测试(四)
一、选择题:(本大题共12道小题,每题5分)
1、已知![]() 、
、![]() 都是第一象限角,且
都是第一象限角,且![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)以上都不对
(D)以上都不对
2、若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的最大值是( )
的最大值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3、在正六边形ABCDEF中,O为中心,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4、若直线![]() 按向量
按向量![]() 平移后得到
平移后得到![]() ,则
,则![]()
(A)只能是![]() (B)只能是
(B)只能是![]() (C)
(C)![]() 或
或![]() (D)有无数个
(D)有无数个
5、已知![]() =
= ![]()
![]() ,设
,设![]() ,
,![]() ,
,![]() ,那么p,q,r的大小关系是( )
,那么p,q,r的大小关系是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6、已知![]() 是不等的正数,则在四个数 ①
是不等的正数,则在四个数 ①![]() ,②
,②![]() ,③
,③![]() ,④
,④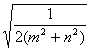 中,最小的一个是( )
中,最小的一个是( )
(A) ① (B) ② (C) ③ (D) ④
7、设向量![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8、已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 或
或![]()
9、下列条件中,不能确定三点A、B、P共线的是 ( )
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D)![]()
10、某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金 ( )
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金 ( )
(A)大于![]() (B)小于
(B)小于![]() (C)大于等于
(C)大于等于![]() (D)小于等于
(D)小于等于![]()
11、若![]() ,使关于x的方程
,使关于x的方程![]() 有解的正数a的取值范围是( )
有解的正数a的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12、下面四个命题:(1)当![]() 时,若
时,若![]() ,则
,则![]()
(2)给定三个向量![]() 、
、![]() 、
、![]() ,则
,则![]()
(3) ![]() 在
在![]() 方向上的投影等于
方向上的投影等于![]() 在
在![]() 方向上的投影与
方向上的投影与![]() 在
在![]() 方向上的投影之和
方向上的投影之和
(4)![]() 、
、![]() 是非零向量,则
是非零向量,则![]() 与
与![]() 垂直的充要条件是
垂直的充要条件是![]()
其中正确的命题个数是( )(A)1个 (B)2个 (C)3个 (D)4个
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题:(本大题共4道小题,每题4分)
13、已知![]() ,
,![]() ,若
,若![]() 与
与![]() 的夹角为锐角,则
的夹角为锐角,则![]() 的取值范围为
的取值范围为
14、不等式![]() 的解集是
的解集是![]()
15、已知![]() ,且
,且![]() ,则
,则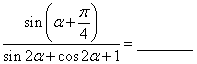
16、函数![]() ,给出以下四个论断:
,给出以下四个论断:
①它的周期为![]() ②它的图象关于直线
②它的图象关于直线![]() 对称
对称
③它的图象关于点![]() 对称 ④在区间
对称 ④在区间![]() 上是增函数
上是增函数
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题![]()
三、解答题:(本大题共6道小题,要求写出必要的解题过程)
17、解关于![]() 的不等式
的不等式![]() .
.
18、平行四边形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
19、已知![]() 为坐标原点,
为坐标原点,![]()
![]() ,
,![]()
![]()
(1)求![]() 的单调递增区间(2)若
的单调递增区间(2)若![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,求
,求![]() 、
、![]() 的值.
的值.
20、在![]() 中,已知
中,已知![]() ,
,![]()
(1)若![]() ,求
,求![]() 、
、![]() 、
、![]()
(2)求![]() 的最大角的弧度数.
的最大角的弧度数.
21、某体育馆拟用运动场的边角地建一个 矩形的健身室.如图,
矩形的健身室.如图,![]() 是一块边长为
是一块边长为![]() 米的正方形地皮,扇形
米的正方形地皮,扇形![]() 是运动场的一部分,其半径为
是运动场的一部分,其半径为![]() 米,矩形
米,矩形![]() 就是拟建的健身室,其中
就是拟建的健身室,其中![]() 、
、![]() 分别在
分别在![]() 和
和![]() 上,
上,![]() 在
在![]() 上,设矩形
上,设矩形![]() 的面积为
的面积为![]() ,
,![]() ,请将
,请将![]() 表示为
表示为![]() 的函数,并指出当点
的函数,并指出当点![]() 在
在![]() 的何处时,该健身室的面积
的何处时,该健身室的面积
最大,最大面积是多少?
22、设![]() ,
,![]() ,其中
,其中![]() ,且
,且![]()
(1)求证:![]() ;(2)求证:函数
;(2)求证:函数![]() 与
与![]() 的图象有两个不同的交点
的图象有两个不同的交点
(3)设![]() 与
与![]() 图象的两个不同交点为
图象的两个不同交点为![]() 、
、![]() ,求证:
,求证:![]()
高一下综合测试(四)
一、选择题:DBADA DCBDA CB
二、填空题:13、![]() 且
且![]() 14、
14、![]()
15、![]() 16、①②
16、①②![]() ③④ 或 ①③
③④ 或 ①③![]() ②④
②④
三、解答题:
17、(1)当![]() 时,原不等式转化为
时,原不等式转化为![]() 解得
解得![]() …… 2分
…… 2分
(2)当![]() 时,原不等式转化为
时,原不等式转化为![]() …… 3分
…… 3分
① 当![]() 时,转化为
时,转化为![]()
当![]() ,即
,即![]() 时 ,解得
时 ,解得 ![]() 或
或![]() ,当
,当![]() ,即
,即![]() 时, 解得
时, 解得 ![]()
当![]() ,即
,即![]() 时 解得
时 解得 ![]() 或
或![]() …… 7分
…… 7分
② 当![]() 时,转化为
时,转化为![]() 解得
解得 ![]() …… 10分
…… 10分
综上所述,当![]() 时解集为
时解集为![]() ,当
,当![]() 时解集为
时解集为![]()
当![]() 时解集为
时解集为![]() ,当
,当![]() 时解集为
时解集为![]()
当![]() 时解集为
时解集为![]() …… 12分
…… 12分
18、![]()
![]() …… 5分
…… 5分
由已知得:
![]()
![]() …… 10分
…… 10分
![]()
![]() …… 12分
…… 12分
19、(1)![]() …… 2分
…… 2分
![]() 时递增区间
时递增区间![]() …… 4分
…… 4分
![]() 时递增区间
时递增区间![]() …… 6分
…… 6分
(2)![]() …… 12分
…… 12分
20、(1)![]() …… 4分
…… 4分
(2)由已知 ![]()
![]()
![]() ,
,![]()
所以![]() 为最大边,
为最大边,![]() 最大
…… 8分
最大
…… 8分
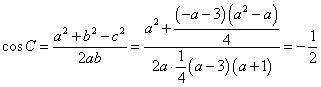
又![]() 因而
因而![]() …… 12分
…… 12分
21、![]() …… 4分
…… 4分
整理得![]()
设![]() 则
则![]()
![]()
![]() ……8分
……8分
当![]() ,即
,即![]() 时
时 ![]() …… 10分
…… 10分
答:当![]() 在
在![]() 的端点E或F处时,健身室面积最大,最大面积500平方米.… 12分
的端点E或F处时,健身室面积最大,最大面积500平方米.… 12分
22、(1)由![]() ,
,![]() 可知
可知![]()
由![]() 得
得![]() 即
即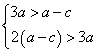 ,
, ![]() 且
且![]() … 4分
… 4分
(2)由![]() 得
得 ![]()
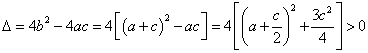
故有两个不同交点 …… 8分
(3)![]()
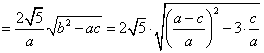
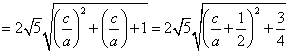
又 ![]() 从而得证
……14分
从而得证
……14分