高一数学下综合测试（一）
一、选择题（本大题共12小题,每小题5分,共60分.）
1、sin(－
)的值等于
( )
A. 
B. －
C. 
D. －
2、已知角α的终边过点P(－4,3) ，则
的值是（ ）
A、－1 B、1 C、
D、 
3、已知︱cos
︱＝-cos，︱tan︱＝tan，则
在 （ ）
A、第二、四象限 B、第一、三象限
C、第一、四象限或终边在x轴 D、第二、四象限或终边在y轴上
4、 
=
（ ）
A．
B．
C．—
D．—
5、 函数
的定义域是
（
）
A．
B．
C．
D．
6、已知8sin
＋5cosβ=6,
8cos＋5sinβ=10，则sin(＋β)的值是（ ）
A、
B、
C、－
D、±
7、若
（ ）
（A）
（B）
（C）
（D）
8、把函数
的图象上所有的点的横坐标缩小到原来的一半，纵坐标保持不变，然后把图象向左平移
个单位长度，得到新的函数图象，那么这个新函数的解析式为（ ）
A．
B.
C．
D. 
9、设
，
，
，则有( )
A．
B．
C．
D．
10、关于函数y=sinxcos(2
－2x)－sin(
+x)sin(+2x)的最小正周期
和奇偶性, 下列叙述正确的是( )
A. 周期为2的奇函数 B. 周期为2的偶函数
C. 周期为
的奇函数 D. 周期为的偶函数
11.若
，且
，则
等于（ ）
A．
B．
C．
D．
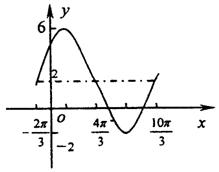
12.函数
的图象如图所示，
|
、
、b的取值可以是（ ）
A．
B．
C．
D．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题：本大题共4小题，每小题4分，共16分
13、已知
。
14、 函数y＝
－2cosx的最小值是___
____________。
15、已知
，求
的值是
。
16、 关于函数f(x)＝4sin(2x＋
), (x∈R)有下列命题：
①y＝f(x)是以2π为最小正周期的周期函数；② y＝f(x)可改写为y＝4cos(2x－
)；
③y＝ f(x)的图象关于(－，0)对称；④
y＝ f(x)的图象关于直线x＝－对称；
其中真命题的序号为 。
三、解答题（本大题共6小题，共74分）
17.（本小题12分）已知tan（
－
）＝3，
求（1）
（2）
18、（本小题12分）已知
，
（1）求
的值； （2）求
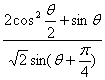的值。
19、（本小题13分）已知
，求
的值。
20、（本小题满分13分）已知函数
，求：
（1）求f(x)的最大值及取得最小值时对应的x的集合.
（2）函数图象的对称中心坐标；（3）函数图象的对称轴。
21．（本题满分13分）已知函数f(x)＝2asin2x＋2
，
(a＞0,x∈R),当x∈[0，
]时，其最大值为6，最小值为3，
(1) 求函数的最小正周期；(2)写出函数的单调递减区间；(3)求a,b的值；
22．（本题满分12分）已知函数
的图象，它与y轴的交点为（
），它在y轴右侧的第一个最大值点和最小值点分别为
。（1）求函数
的解析式；
（2）该函数的图象可由
的图象经过怎样的平移和伸缩变换得到?
高一下综合测试（一）
一.选择题：B.D.D.D.B.B.D. C.D.C. B.D；二、填空题： 13. -
14. 
15. 
16. ②③ 17. (1) -8 ；(2) 
；18.(1) 
(2)
-4；19. 
20、（1）当f(x)取得最大值2时对应的x的集合为
；当f(x)取得最小值－2时对应的x的集合为
（2）
（3）
21.解：f(x)＝2asin2x＋2
asinxcosx＋a＋b＝a(1－cos2x)＋asin2x＋a＋b
＝2asin(2x－
)＋2a＋b
(1)T＝π
(2)单调减区间为
（3）x∈[0，]时，
2x－∈[－，
]则有：sin(2x－)∈[－
，1]，
由条件：a＋b ＝3，4a＋b＝6,则 a＝1， b＝2为所求。
22．解：（1）由题意可得
由在
轴右侧的第一个最大值点和最小值点分别为
，
得
，∴
从而
又图象与轴交于点
，∴
由于
，∴
函数的解析式为
6分
(2)将函数
的图象向左平移
个单位，得到函数
的图象；再将所得函数的图象纵坐标不变，横坐标伸长为原来的两倍得到函数
的图象；最后将所得函数的图象横坐标不变，纵坐标伸长为原来的3倍得到函数
的图象