高一学分认定考试数学必修4试卷
一.选择题:(共.40分)
1.![]() 的正弦值等于
( )
的正弦值等于
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.215°是 ( )
(A)第一象限角 (B)第二象限角
(C)第三象限角 (D)第四象限角
3.角![]() 的终边过点P(4,-3),则
的终边过点P(4,-3),则![]() 的值为 (
)
的值为 (
)
(A)4 (B)-3 (C)![]() (D)
(D)![]()
4.若sin![]() <0,则角
<0,则角![]() 的终边在
( )
的终边在
( )
(A)第一、二象限 (B)第二、三象限
(C)第二、四象限 (D)第三、四象限
5.函数y=cos2x的最小正周期是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.给出下面四个命题:①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() 。其中正确的个数为 ( )
。其中正确的个数为 ( )
(A)1个 (B)2个 (C)3个 (D)4个
7.向量![]() ,
,![]() ,则
( )
,则
( )
(A)![]() ∥
∥![]() (B)
(B)![]() ⊥
⊥![]()
(C)![]() 与
与![]() 的夹角为60° (D)
的夹角为60° (D)![]() 与
与![]() 的夹角为30°
的夹角为30°
8. 化简![]() 的结果是
( )
的结果是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.
函数![]() 是
( )
是
( )
(A)
周期为![]() 的奇函数 (B)
周期为
的奇函数 (B)
周期为![]() 的偶函数
的偶函数
(C) 周期为![]() 的奇函数 (D)
周期为
的奇函数 (D)
周期为![]() 的偶函数
的偶函数
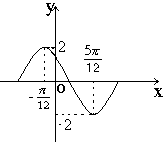 10.函数
10.函数![]() 在一个周期内的图象如下,此函数的解析式为
( )
在一个周期内的图象如下,此函数的解析式为
( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二.填空题:(共20分,请将答案直接填在题后的横线上。)
11.已知点A(2,-4),B(-6,2),则AB的中点M的坐标为 ;
12.若![]() 与
与![]() 共线,则
共线,则![]() = ;
= ;
13.若![]() ,则
,则![]() = ;
= ;
14.已知![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,那么
,那么![]() =
。
=
。
15.函数![]() 的值域是
的值域是![]() ;
;
三.解答题(共.40分,解答题应写出文字说明、演算步骤或证明过程.)
16. 用五点作图法画出函数 ![]() 的简图.
的简图.
17.求值:(1)![]() ; (2)
; (2)![]()
18.
已知![]() 为锐角,且cos
为锐角,且cos![]() =
=![]() ,cos
,cos![]() =
=![]() ,求
,求![]() 的值.
的值.
19.设![]() ,
,![]() ,
,![]() ,
,![]() ∥
∥![]() ,试求满足
,试求满足
![]() 的
的![]() 的坐标(O为坐标原点)。
的坐标(O为坐标原点)。
20.已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转q角得到向量
绕其起点沿逆时针方向旋转q角得到向量![]() ,叫做把点B绕点A逆时针方向旋转q角得到点P.
,叫做把点B绕点A逆时针方向旋转q角得到点P.
(1)已知平面内点A(2,1),点B(![]() ,
,![]() ).把点B绕点A沿逆时针方向旋转
).把点B绕点A沿逆时针方向旋转![]() 后得到点P,求点P的坐标;
后得到点P,求点P的坐标;
(2)设平面内曲线C上的每一点绕坐标原点O沿顺时针方向旋转![]() 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
诸中2006-2007学年度高一学分认定考试
数学必修4答题卷
班级: 姓名: 编号: 分数:
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题:
11.____________ 12.___________ 13._________
14______________ 15_____________
三.解答题:
16.
17
18.
19.
20.
参考答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | D | A | B | B | B | C | A |
二.填空题:
11. (-2,-1) 12. _ -6 __ 13._ -3 14. ![]() 15____[-1,3] ___
15____[-1,3] ___
三.解答题:
16.略
17.解:(1)![]()
(2)原式=![]()
=![]()
18.

19. 解:设![]() ,由题意得:
,由题意得: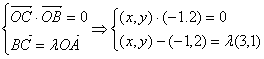
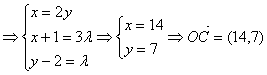
![]()
20. 解:(1)
设P(x,y), 则![]() ,
,
![]() ,
,
由题意,得:
![]()
∴ x-2=6,y-1=2, ∴x=8,y=3.
(2)设P(x,y)是曲线C上任意一点,![]() 绕绕坐标原点O沿顺时针方向旋转
绕绕坐标原点O沿顺时针方向旋转![]() 后,点P的坐标为(x’,y’),则:
后,点P的坐标为(x’,y’),则:
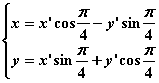 即
即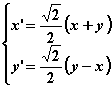
又因为![]() 所以
所以 ![]()
化简得: ![]() .
.