1.5函数
的图象
一、情景导入：
1．函数y=Asin(ωx+φ)的图像与y=sinx的图像关系.
(1)振幅变换：函数y=Asinx(A＞0,且A≠1)的图像，可以看作是y=sinx图像上所有点的纵坐标伸长(A＞1)或缩短(0＜A＜1)到原来的A倍(横坐标不变)而得到的.这种变换叫振幅变换，它实质上是纵向的伸缩.
(2)周期变换：函数y=sinωx(ω＞0,且ω≠1)的图像，可以看作是把y=sinx的图像上各点的横坐标都缩短(ω＞1)或伸长(0＜ω＜1
到原来的
倍(纵坐标不变)而得到的，由y=sinx的图像变换为y=sinωx的图像，其周期由2π变
.这种变换叫做周期变换.它实质上是横向的伸缩.
(3)相位变换：函数y=sin(x+φ)(φ≠0)的图像，可以看作是把y=sinx的图像上各点向左(φ＞0)或向右(φ＜0)平移｜φ｜个单位而得到的.这种由y=sinx的图像变换为y=sin(x+φ)的图像的变换，使相位x变为x+φ,我们称它为相位变换.它实质上是一种左右平移变换.
应用振幅变换、周期变换、相位变换(左右平移变移)和上下平移变换可由y=sinx的图像得到y=Asin(ωx+φ)+k的图像.
2．设f、t、h分别表示相位变换，周期变换，振幅变换，变换作图法共有以下不同的程序：
(1)f→t→h;(2)f→g→t(3)t→h→f;(4)t→f→h;(5)h→f→t;(6)h→t→f
3.y=Asin(ωx+φ)(A＞0，ω＞0)与简谐振动
在物理学中，y=Asin(ωt+φ)(A＞0,ω＞0),其中t∈［0，+∞)，表示简谐振动的运动方程.这时参数A，ω，φ有如下物理意义：
A称为振幅，它表示振动时物体离开平衡位置的最大距离.
T=称为周期，它表示振动一次所需的时间(亦即函数y的最小正周期).
f=
= 
称为振动的频率，它表示单位时间内往复振动的次数，ωt+φ叫做相位，当t=0时的相位，即φ称为初相.
二、感受理解：
1．请用五点法作出
在一个周期上的简图
2．试说明y=cosx的图像经怎样的变换可得到y=3cos(3x+
)+1的图像?
3．指出将y=sinx的图像变换为y=sin(2x+
)的图像的两种方法.
4．函数f(x)的横坐标伸长到原来的两倍，再向左平移个单位，所得到的曲线是y=
sinx的图像，试求函数y=f(x)的解析式.
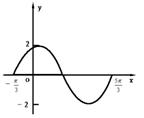
5．如图是函数y=Asin(ωx+φ)图像一段，函数定义域是 ，值域是 ，周期是 ，振幅是 ，函数解析式是 ，当x= 时y取最大值= ，当x= ,y取最小值 ，x= 时，y=0，函数递减区间是 .
三、迁移拓展：
6．函数y=Acos(ωx+φ)(A≠0,ω≠0)的奇偶性( )
A.仅与A有关 B.仅与ω有关 C.仅与φ有关 D.与A、ω、φ有关
7. 函数y=sin2x的图像向左平移
所得曲线的对应函数式( )
A.y=sin(2x+)
B.y=sin(2x-) C.y=sin(2x+
) D.y=sin(2x-)
8.得到函数y=sin(2x-)的图像，只需将y=sin2x的图像( )
A.向左移动 B.向右移动 C.向左移动 D.向右移动
9.函数y=sin(2x-)的单调递减区间是( )
A.［kπ+
,kπ+
π］ B.［kπ-
π,kπ+］
A.［kπ-,kπ+］ D.［kπ+,kπ+
π］(k∈Z)
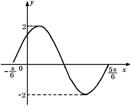
10. 函数
＝Asin(ωx+φ)的一个周期内的图象如图，则的表达式为( )
A．y＝2sin(x+) B．y＝2sin(x+) C．y＝2sin(2x+) D．y＝2sin(2x+)
11．函数
的振幅是 ；周期是 ．
12．函数y=sin(3x-)的定义域是 ，值域是 ，周期是 ，振幅是 ，频率是 ，相位是 ，初相是
12. 要得到函数y=3cos(2x-
π)的图像C，需要将函数y=3sin2x的图像C0经过平移得到，则平移路程最小的长度是 单位.
14.已知函数f(x)=sin(
x+
),使f(x)的周期在(
，
)内，则正整数k= .
15.给出下列命题：
(1)函数y=sinx在第一、四象限都是增函数；(2)函数y=cos(ωx+φ)的最小正周期为
；
(3)函数y=sin(x+
π)是偶函数；
(4)函数y=sin2x的图像向左平移个单位，得到y=sin(2x+)的图像.
其中正确的命的序号是 .
16．写出下列函数图象的解析式
（1）将函数y=sinx的图象上所有点向左平移
个单位，再把所得图象上各点的横坐标扩大为原来的2倍，得到所求函数的图象。
（2）将函数y=cosx的图象上所有点横坐标缩为原来的一半，纵坐标保持不变，然后把图象向左平移
个单位，得到所求函数的图象。
17.已知y=Asin(ωx+φ)(A＞0,ω＞0,0＜φ＜π的最小正周期为
，最小值为-2，且过点(
π，0)，求它的表达式.
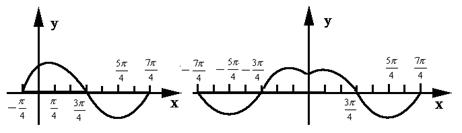
18.用“五点法”作出函数f(x)=sin(x+)一个周期的图像，并画出f(｜x｜)的图像.
19．说明函数
的图像可以由函数
的图像经过怎样的变换得到。
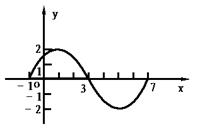
20．如图，是正弦函数f(x)=Asin(ωx+φ)(A＞0,ω＞0)的一个周期的图像. (1)写出f(x)的解析式；
(2)若g(x)与f(x)的图像关于直线x=2对称，写出g(x)的解析式.
四、实践应用：
21．函数f(x)=Msin(ωx+φ)(ω＞0)在区间［a,b］上是增函数，且f(a)=-M,f(b)=M，则函数g(x)=Mcos(ωx+φ)在［a,b］上( )
A.是增函数 B.是减函数 C.可以取得最大值M D.可以取得最小值-M
22．函数y＝Asin(ax+b)的图象与函数y＝Acos(ax+b)的图象在区间［m,m+
］(a＞0)( )
A.可能没有交点 B.一定有两个交点 C.至少有一个交点 D.只有一个交点
参考答案：
1.5函数的图象
二、感受理解
1． 略 2． 略
3． （1） y=sinx
y=sin2x
y=sin［2(x+)］
（2） y=sinx
y=sin(x+)
y=sin(2x+).
4．y=-cos2x 5． ［2kπ-,2kπ+
］(k∈Z),［-2,2］,T=2π,2，
y=2sin(x+),x=+2kπ,k∈Z,2,x=
π+2kπ,k∈Z时，-2，x=-+2kπ, +2kπ, +2kπ时,y=0,［+2kπ, 
+2kπ］(k∈Z)
三、迁移拓展：
6．Ｃ 7．Ｃ 8．Ｄ 9．Ｄ 10．D 11．2 ,
12．R，［-，］T=,A=,f=
,3x-,- 13．向左平移
14．15,16,17 15．(3) 16． （1）
(2)
17．y=2sin(3x+)
18．
19．可先把的图像上所有点向右平移
个单位，得到
的图像，再把图像上的所有点的横坐标伸长到原来的2倍（纵坐标不变），从而得到的图像。
20． (1)f(x)=2sin(x+) (2)g(x)=2sin(x-)
四、实践应用：
21．C 22． C.