函数单元测试

函数单元测试

1.的值是(　　)

A.2　　　　　　 B.　　　　　　　　C.1　　　　　　 D.

【解析】

【答案】D

2.已知f(x)=x+1,若f(x+1)的图象关于直线x=2对称图象对应的函数为g(x)，则g(x)为(　　)

A.6－x　　　　　B.x－6　　　　　　　C.x－2　　　　　D.－x－2

【解析】由f(x)=x+1可得f(x+1)=x+2，f(x+1)的图象关于x=2对称的图象对应的函数g(x)=　　　6－x.

【答案】A

3.若f(x)=(e^x－e^－x),g(x)=  (e^x+e^－x),则f(2x)等于(　　)

A.2f(x)　　　　　　　　　　　　　　 B.2g(x)

C.2［f(x)+g(x)］　　　　　　　　　　D.2f(x)·g(x)

【解析】2f(x)·g(x)=2·(e^x－e^－x)·(e^x+e^－x)= (e^2x－e^－2x)=f(2x).

【答案】D

4.设F(x)=lnx,f(x)=1－x²,则函数g(x)=F［f(x)］的定义域是(　　)

A.(0,+∞)　　　　　　　　　　　　　　　 B.(－∞,+∞)

C.｛x｜x∈R且x≠±1｝　　　　　　　D.(－1，1)

【解析】1－x²＞0x＜1,

∴x∈(－1,1).

【答案】D

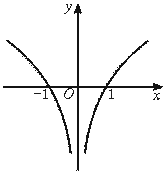
5.函数f(x)的图象如图2-31所示，则不等式xf(x)＞0的解集是(　　)

A.(－∞，－1)∪(0，1)　　　　　　　　　　　 B.(－1，0)∪(1，+∞)

C.(－∞，－1)∪(1，+∞)　　　　　　　　 D.(－1，0)∪(0，1)

【解析】xf(x)＞0

由图象知f(x)＞0x＜－1或x＞1，f(x)＜0－1＜x＜0或0＜x＜1

∴xf(x)＞0x＞1或－1＜x＜0.

【答案】B

6.函数y=的图象一定(　　)

A.关于点(－2，3)对称　　　　　　　　　　B.关于点(2，－3)对称

C.关于直线x=－2对称　　　　　　　　　　D.关于直线y=－3对称

【解析】由y==3－.

【答案】A

7.设a=log_0.70.8,b=log_1.10.9,c=1.1^0.9，则(　　)

A.a<b<c　　　　　　　　　　　　　　　　 B.b<c<a

C.b<a<c　　　　　　　　　　　　　　　　 D.c<a<b

【解析】∵log_1.10.9<0<log_0.70.8<1<1.1^0.9,∴b<a<c

【答案】C

8.函数f(x)在区间[1，4]上是减函数，且f(-x)=f(x)，下列不等式成立的是（　 ）

A.f()>f(-)

B.f(-1)<f(3)

C.f(-π)>f(π)

D.f(2)<f(-3)

【答案】A

9.函数y=2^－x－1－m的图象与x轴有交点时，m的范围是(　　)

A.－1≤m<0　　　　　　　　　　　　　　　B.0≤m≤1

C.m≥1　　　　　　　　　　　　　　　　　D.0<m≤1

【解析】令2^－x－1－m=0即m=2^－x－1

由－x－1≤0,得0<2^－x－1≤1,即0<m≤1.

【答案】D

10.函数y=的反函数(　　)

A.在(0，+∞)上递减，在(－∞,0)上也递减

B.在(0，+∞)上递减，在(－∞,0)上递增

C.在(0，+∞)上递增，在(－∞,0)上也递增

D.在(0，+∞)上递增，在(－∞,0)上递减

【解析】∵函数y=在R上递增.

∴其反函数在R上也递增.

因此在(－∞,0)和(0，+∞)上递增.

【答案】C

11.将函数y=2^x的图象(　　)，再作关于直线y=x对称的图象，可得到函数y=log₂(x+1)的图象.(　　)

A.先向左平移一个单位

B.先向右平移一个单位

C.先向上平移一个单位

D.先向下平移一个单位

【解析】y=2^x的图象向下平移一个单位得到y=2^x－1的图象，而y=2^x－1的反函数为y=log₂(x+1).

【答案】D

12. 设f(x)是R上的函数，且f(-x)=-f(x),当x∈[0，+∞）时，f(x)=x(1+),即么当x∈（-∞，0）时，f(x)=__________。

【答案】x(1-)

13.已知f(x)=4^x－2^x+1,则f^－1(0)=______.

【解析】令f^－1(0)=a,则f(a)=0

∴4^a－2^a+1=0,即2^2a=2^a+1

∴a=1,即f^－1(0)=1.

【答案】1

14.求下列函数的值域：

(1)y=；　　

(2)y=.

【解】 (1)由y=得 x=,又分母不为0，∴原函数的值域为｛y｜y≠－,y∈R｝.

(2)由原式得(y－1)x²+(1＋y)x+y－1=0,

(ⅰ)当y=1时，x=0.

(ⅱ)当y≠1时，

∵x∈R,∴Δ=(y+1)²－4(y－1)²≥0,即3y²－10y+3≤0,

∴≤y≤3(y≠1),综合(ⅰ)(ⅱ)得y∈［,3］.

【说明】 (1)、(2)两题还有另外解法.

15.已知f(x)=lg(x²－2x+m)，其中m∈R为常数

(1)求f(x)的定义域；

(2)证明f(x)的图象关于直线x=1对称.

【解】 (1)由x²－2x+m＞0得(x－1)²＞1－m

当1－m＜0,即m＞1时，x∈R

当1－m≥0,即m≤1时，x＜1－或x＞1+,

故当m＞1时，f(x)定义域为R.

当m≤1时f(x)定义域为(－∞,1－)∪(1+,+∞)

(2)设A(x₀，f(x₀))为f(x)图象上任意一点，则A点关于直线x=1的对称点为A′(2－x₀,f(x₀))

∵f(2－x₀)=lg［(2－x₀)²－2(2－x₀)+m］=lg(x₀²－2x₀+m)=f(x₀)

∴A′点也在f(x)图象上

由A点的任意性知f(x)的图象关于直线x=1对称.

16.求函数f(x)=log_0.5｜x²－x－12｜的单调区间.

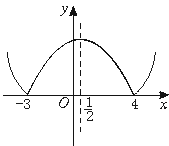【解】 设u=｜x²－x－12｜,

观察其图象(如图)知，函数u的递增区间为(－3,)和(4,+∞)，此即f(x)的递减区间为(－3，)和(4，＋∞)，

∴u的递减区间为(－∞,－3)和[,4],此即为f(x)的递增区间.

17.若函数f(x)=log_ax(其中a＞0且a≠1)在x∈［2，＋∞）上总有｜f(x)｜＞1成立，求a的取值范围.

【解】 若a＞1，x≥2时，log_ax＞0，

由｜f(x)｜＞1得f(x)＞1，

即log_ax＞1恒成立.

∴x＞a恒成立，

∴1＜a＜2.

若0＜a＜1，x≥2时log_ax＜0，

由｜f(x)｜＞1得f(x)＜－1.

即log_ax＜－1恒成立，

也即x＞恒成立，

∴＜2.∴＜a＜1，

综上，a的取值范围为(，1)∪(1，2).

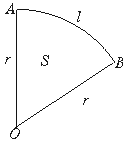18.某人要在自己房间的山墙上订制一个扇形框架装饰房间，现有10尺竹条作为周边的装饰材料，问如何设计扇形半径r，可使扇形的面积S最大？(注：扇形面积公式S_扇形=lr，l为弧长，r为半径)

【解】 如图所示，扇形OAB中OA=OB=r，=l，

依题意2r+l=10,∴l=10－2r＞0,即r＜5

又∠AOB＜360°即l＜2πr,∴10－2r＜2πr.

∴＜r＜5.

又S=lr= (10－2r)r

=－r²+5r=－(r－)2+ (＜r＜5）

∴当r= (尺)时S_最大= (平方尺)

【答】 取扇形半径为2.5尺，弧长为5尺时可使扇形面积最大.

19.已知函数f(x)=.

(1)判断f(x)的单调性，并加以证明.

(2)求f(x)的反函数.

【解】 (1)∵x∈R时,2^x+1＞0恒成立.

∴f(x)的定义域是R.

f(x)在R上是增函数，证明如下：

设x₁,x₂∈R,且x₁＜x₂,则0＜2^x1＜2^x2

∴f(x₁)－f(x₂)=

=

=.

∵2^x1－2^x2＜0,2^x1+1＞0,2^x2+1＞0

∴f(x₁)－f(x₂)＜0,即f(x₁)＜f(x₂)

∴f(x)在R上是增函数.

(2)由y=,解得2^x=

∵2^x＞0,∴＞0,即 －1＜y＜1

∴x=log₂ (－1＜y＜1)

∴f(x)的反函数为

f^－1(x)=log₂ (－1＜x＜1＝.