高一数学单元同步练习

高一数学单元同步练习

一、选择题

1．在等差数列中，，则（　　）

A．-22　　　 B．-24　　　 C．60　　　　　　D．64

2．若数列{a_n}的前n项和S_n=n²+1，则这个数列前三项分别为

  （A）1，3，5　　　 （B）2，5，7　　 （C）2，－5，－7　　（D）2，3，5

3、设{a_n}递增等差数列，前三项的和为12，前三项的积为48，则它的首项为　　

A、1　　　　 　　 B、2　　 　　　　　C、4　　 　　　　 D、6

4．已知数列{a_n}的通项公式a_n=－3n+50，则当前n项和S _n最大时，n的值是　 （A）15　　　　　　 （B）16　　　　  （C）17　　　　　　  （D）18

5、在等差数列{a_n}中，若a₂+a₆+a₁₀+a₁₄=32，则a₈等于

（A ）2　　 （B）4　　 （C）8　　  （D）16

6、等差数列{}的公差为，则的值为（　　）

（A）85　 （B）75　 （C）　 （D）60

7. 已知为等差数列，公差，，则（　　）

A. 60　　　B. 　　　C. 182　　　D.

8、等差数列{a_n}的前m项和为30，前2m项和为100，则它的前3m项和为

A.30　　　　B.170　　C.210　　D.260

9、.已知等差数列{a_n}的公差为正数，且a₃·a₇=－12,a₄+a₆=－4,则S₂₀为（　　）

A.180　　　　 B.－180　　　　 C.90　　　　　　　　　　 D.－90

10、.设a_n=－n²+10n+11,则数列{a_n}从首项到第几项的和最大（　　）

A.第10项　　　B.第11项　　　C.第10项或11项　　　　D.第12项

11. 等差数列中的前12项的和为，其中奇数项之和与偶数项之和的比为，则的公差（　　）

A. 10　　　 B. 30　　　C. 5　　　D. 15

12.已知数列{a_n}中，a₁=1,a_n+1=a_n(n∈N^*),则a_n等于

A.n+1　　　　　　B.　　　　 C.n+2　　　　　　 D.n+

二、填空题

13．若一个等差数列的前3项和为34，最后3项的和为146，所有项的和为780，则这个数列的项数为_______________。

14．若等差数列中，，表示数列的前n项和，且，则取最大值时n=__________________。

15.等差数列{a_n},{b_n}的前n项和分别为S_n、T_n,若=,则=_________.

16、等差数列{a_n}中，S_n是其前n项之和，且S₆<S₇，S₇>S₈，则：①数列{a_n}中，前七项递增，从第八项开始递减；②S₉一定小于S₆；③a₁是各项中最大的项；④S₇不一定是S_n的最大值。

其中正确的命题是　　　　　　　　  。（将正确命题的序号都填上）

三、解答题

17、等差数列中, ,,求其通项及前项和.

18、已知三个数成等差数列，其和为15，其平方和为83，求此三个数

19．设为等差数列，已知a₃=11,a₈=31.（1）求a_n；（2）若S_n为数列的前n项和，T_n为数列的前n项和，求T_n。

20、（本小题满分12分）设等差数列{a_n}的前n项和为S_n,已知a₃=12, S₁₂>0,S₁₃<0.

(1)求公差d的取值范围；

（2）指出S₁，S₂，S₃…S₁₂中哪一个值最大？并说明理由.

21、已知数列是等差数列，且,。　　

（1）求数列的通项公式。（2）令。求数列的前项和。

22.（本小题满分12分）已知数列{a_n}的前n项和为S_n，且满足a_n+2S_n·S_n－1=0(n≥2),a₁=.

(1)求证：{}是等差数列；（2）求a_n表达式；

（3）若b_n=2(1－n)a_n(n≥2),求证：b₂²+b₃²+…+b_n²<1.

【解】 （1）∵－a_n=2S_nS_n－1,∴－S_n+S_n－1=2S_nS_n－1(n≥2)

S_n≠0,∴－=2,又==2,∴{}是以2为首项，公差为2的等差数列.

（2）由（1）=2+(n－1)2=2n,∴S_n=

当n≥2时，a_n=S_n－S_n－1=－

n=1时，a₁=S₁=,∴a_n=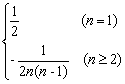

(3)由（2）知b_n=2(1－n)a_n=

∴b₂²+b₃²+…+b_n²=++…+<++…+

=(1－)+(－)+…+(－)=1－<1.