高一数学第18周每周一练

高一数学第18周每周一练（必修2第一、二、三章3.1～3.2）14-5-13

1、直线的倾斜角是（　　　）A.30⁰　　 B.60⁰C.120⁰ D.135⁰

2、下列命题为真命题的是（　　）

A.平行于同一平面的两条直线平行；　B.与某一平面成等角的两条直线平行；

C.垂直于同一平面的两条直线平行；　D.垂直于同一直线的两条直线平行。

3、下列命题中错误的是：（　 ）

A.　　　如果α⊥β，那么α内一定存在直线平行于平面β；

B.如果α⊥β，那么α内所有直线都垂直于平面β；

C’

C.如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；

D.如果α⊥γ，β⊥γ，α∩β＝l,那么l⊥γ.

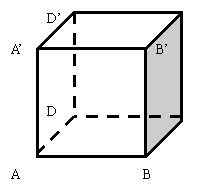
4、右图的正方体ABCD-A^’B^’C^’D^’中,异面直线AA^’与BC所成的角是（　 ）

A.　30⁰　　　 B.45⁰　　　　 C.　60⁰　　　　 D. 90⁰

5、右图的正方体ABCD- A^’B^’C^’D^’中，二面角D^’-AB-D的大小是（　　）

C

A. 30⁰　 　　　 B.45⁰　　　　　 C.　60⁰　　　D. 90⁰

6、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则（　　）

A.a=2,b=5;　　 B.a=2,b= -5;　　　C.a= -2,b=5;　　 D.a= -2,b= -5.

7、若三直线2x+3y+8=0，x－y－1=0和x+ky=0相交于一点，则k＝（　）

A.－2　　 B.　　  C.2　　　　D.

8、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是（　　）

A . 4x+3y-13=0　　  B.　 4x-3y-19=0　 C.　3x-4y-16=0　　　D .　3x+4y-8=0

9、如果AB＞0，BC＞0，那么直线Ax—By—C=0不经过的象限是（　 ）

A.第一象限　　　 B.第二象限　　　 C.第三象限　　　D.第四象限；

10、正方体的全面积为a,它的顶点都在球面上，则这个球的表面积是：（　　）

A.　  B.　　　 C.　　  D.

11、光线由点P（2，3）射到直线上，反射后过点Q（1，1），则反射光线所在的直线

方程为（　 ）

 A、　B、　C、　D、

12、已知直线与互相垂直，垂足为（1，c）,则的值为（　 ）

 A.－4　　 B.20　　　 C.0　　　　 D.24

13、已知点A（x,5）关于点（1，y）的对称点（-2，-3），则点P（x，y）到原点的距离是（　）

 A.4　　 B.　　  C.　　  D.

14、直线恒过一定点，则此点是（　）

 A.（1，2）　 B.（2，1）　　 C.（1，-2）　　 D.（-2，1）

15、两直线与x轴相交且能构成三角形，则m满足的条件是

A. m≠ 0 且 m≠ －２　　　B. m≠ 0且m≠－3

C. m≠ －２且m≠－3　　　D. m≠ 0 且 m≠ －２且 m≠－3

二、填空题

16、以原点O向直线l作垂线，垂足为点H（－2，1），则直线l的方程为　　　　　　 .

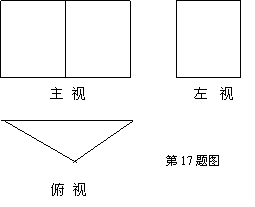
17、下图的三视图表示的几何体是　　　　　　　  .

18、若直线平行，则　　　　　　  .

19、已知Rt△ABC中，AB=AC=a,AD是斜边BC上的高，以AD为折痕使∠BDC成直角，则

∠BAC=　　 .

20、在直线方程y=kx+b中，当x∈[－3，4]时，y∈[－8，13]，则此直线方程是　　　　　　　　　 .

三、解答题（共44分）

21、求经过直线l₁：与直线l₂：的交点M且满足下列条件的

直线方程。

（1）经过原点；（2）与直线平行；（3）与直线垂直

（4）在两坐标轴上的截距相等的直线方程

22、已知三角形ABC的顶点坐标为A（-1，5）、B（-2，-1）、C（4，3），M是BC边上的中点。（1）求AB边所在的直线方程；（2）求中线AM的长。

23、（1）直线l被直线l₁：x－3y+10=0，l₂：2x+y-8=0截得线段恰好被点M（0，1）平分，求直线l得方程.

（2）一条光线从点A（3，2）发出，经x轴反射，通过点B（－1，6），求入射光线和反射光线所在得直线方程.

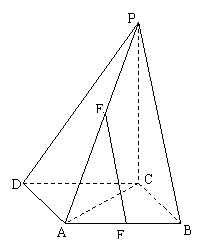23、如图，在平行四边形ABCD中，PC⊥平面ABCD，E,F是PA和AB的中点。

（1）求证： EF平面PBC _;

（2）若EF⊥CD，求证：四边形ABCD是矩形.

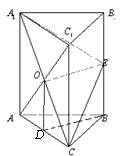
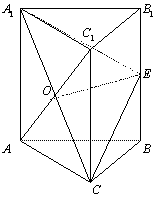24、如图，在正三棱柱ABC-A₁ B₁C₁ 中，（正三棱柱指底面是正三角形，侧棱与底面垂直的三棱柱），E为B B₁ 的中点，O是侧面AC_{1的对角线交点；}

（1）OE∥底面ABC；

（2）求证：截面A₁ EC⊥侧面AC₁.

*25、设直角梯形ABCD，DA⊥AB，在两平行边AB、DC上有两个动点P、Q，直线PQ平分梯形的面积，求证：PQ必过一个定点。

*26．已知正方形的中心为直线和的交点，正方形一边所在直线的方程为

，求其它三边所在的直线的方程.

　　　高一数学第18周每周一练（必修2第一、二、三章）参考答案　 14-5-13

一、选择题 CCBDB　BBABB　CADDD

二、16、2x－ｙ＋５＝０；17、三棱柱；18、；19、60°；20、 y=3x+1或y= -3x+4

21、解：由l₁与l₂的方程联立方程组　　　　　　 x =-1

　　　　　　　　　　　　　　　　  　 解得：　 y =2

∴点M的坐标为（1，－2）

（1）所求直线方程经过(0,0)与M(－1,2),则直线方程为即2x+y=0

(2) 所求直线与直线平行，所求直线的斜率为－2，又经过点M（-1， 2）

则直线方程为y+2=－2（x－1）　 即　 2x+y=0

（3）所求直线与直线垂直，所求直线的斜率为　，又经过点M（-1， 2）

则直线方程为y-2 =（x+1）　 即　 x－2y+5=0

（4）2x+y=0或x+y-1=0

22、解：（1）由两点式写方程得　　　　　　　 ，即　6x-y+11=0

或　 直线AB的斜率为　

　　 直线AB的方程为　　即　6x-y+11=0

（2）设M的坐标为（），则由中点坐标公式得

第24题图

　　　　　　　　  故M（1，1）

23、（1）x+4y-4=0；（2）入射光线和反射光线所在得直线方程分别为2x-y-4=0和2x+y-4=0.

24、（1）证明：

　　　　

 又 故

（2）∵EF⊥CD，AB∥CD ∴EF⊥AB

由（1）知EF∥PB

∴AB⊥PB，　由题意　PC⊥平面ABCD

第25题图

∴AB⊥BC；故四边形ABCD是矩形.

24、提示：（1）取AC的中点D，连接BD、OD；证OE∥BD可得.（2）先证BD⊥侧面AC_{1，结合（1）得}OE⊥侧面AC_1，则得.

25、提示：利用解析法；设AB＝b、AD=c、DC=a，以D原点，DC，DA分别为x、y轴建立平面直角坐标系，设P(x₁,c)，Q（x₂,0），由题意则，得

由中点坐标公式知，则PQ的中点M为（）为定点，即PQ必过一个定点M.

26、x+3y+7=0;3x-y+9=0;3x-y-3=0