高一数学第19周每周一练（必修2第三章） 07-01-06
一、选择题：
1．下列说法正确的是 （ ）
A．若直线
的斜率相等，则直线一定平行；
B．若直线平行，则直线斜率一定相等；
C．若直线中，一个斜率不存在，另一斜率存在，则直线一定相交；
D．若直线斜率都不存在，则直线一定平行。
2．若方程
表示一条直线，则实数
满足 （ ）
A．
B．
C．
D．，
，
3．直线在
轴上的截距都是，在
轴上的截距都是
，则满足 （ ）
A．平行 B．重合 C．平行或重合 D．相交或重合
4．经过点
的直线
到A
、B
两点的距离相等，则直线的方程为 （ ）
A．
B．
C．或 D．都不对
5．已知点
，点
在直线
上，若直线
垂直于直线
，
则点的坐标是 （ ）
A．
B．
C． D．
6．如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不通过 （ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
7．下列说法的正确的是 （ ）
A．经过定点
的直线都可以用方程
表示
B．经过定点
的直线都可以用方程
表示
C．不经过原点的直线都可以用方程
表示
D．经过任意两个不同的点
的直线都可以用方程
表示
8．直线
在
轴上的截距是 （ ）
A．
B．－
C． D．
9．设A、B两点是轴上的点，点
的横坐标为2，且
，若直线
的方程为
，则
的方程为 （ ）
A．
B．
C．
D．
10．若三条直线l1：x－y＝0；l2：x＋y－2＝0; l3：5x－ky－15＝0围成一个三角形，则k的取值范围是 （ ）
A．k
R且k
5且k
1 B．kR且k5且k－10
C．kR且k1且k0 D．kR且k5
11．点
到直线
的距离为 （ ）
A．
B．
C．
D． 
12．若点
到直线
的距离不大于3，则
的取值范围为 （ ）
A．
B．
C．
D．
13．已知两定点A(－3，5)，B(2，15)，动点P在直线3x－4y＋4＝0上，当
＋
取
最小值时，这个最小值为 （ ）
A．5
B．
C．15
D．5＋10
14．直线kx－y＋1＝3k，当k变动时，所有直线都通过定点 （ ）
A．(0，0) B．(0，1) C．(3，1) D．(2，1)
二、填空题：请把答案填在题中横线上．
15．当= 时，直线
，直线
平行．
16．已知△ABC中A
，B
，C
，则△ABC的垂心是
．
17．过点
，且与原点距离等于
的直线方程为
．
18．直线
关于点
的对称直线的方程是
．
三、解答题：解答应写出文字说明、证明过程或演算步骤．
19．已知点
、
，点是轴上的点，求当
最小时的点
的坐标．
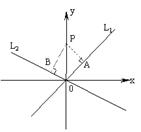
20．已知直线l1：
，l2：
，在两直线上方有一点P（如图），已知
|
与
，再过P分别作l1、l2的垂线，垂足为A、B，
求：
（1）P点的坐标；
（2）AB的值．
21．已知：直线l：
，求：点P（4，5）关于直线
的对称点．
22．已知两直线
,求分别满足下列条件的
、
的值．
（1）直线
过点
，并且直线与直线
垂直；
（2）直线与直线平行，并且坐标原点到、的距离相等．
23．已知直线
，
（1）系数为什么值时，方程表示通过原点的直线；
（2）系数满足什么关系时与坐标轴都相交；
（3）系数满足什么条件时只与x轴相交；
（4）系数满足什么条件时是x轴；
（5）设
为直线上一点，
证明：这条直线的方程可以写成
．
高一数学第19周每周一练参考答案（必修2第三章） 07-01-06
一、CBDCB CDBAB DBAC
二、15．1；16．
；17．
或
；18．
；
三、19．略解：点A关于x轴的对称点为A′（－3，－8），
A′B：2x－y－2=0,A′B与x轴交点为 P（1，0）即为所求.
20．略解（利用待定系数发设出P点的坐标即可）：⑴点P（0，4）；⑵AB=
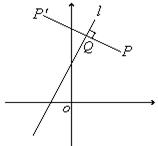21．解：设P关于的对称点为
，直线的斜率为3
∴直线
的方程为：
即：
，设与交于Q点
Q点坐标是
的解，∴Q（1，6）
∵Q是线段的中点
∴
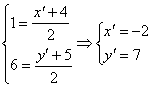∴所求对称点为（－2，7）
22．解：（1）
即
①
又点在上， 
②
由①②解得： 
（2）
∥且的斜率为
.
∴的斜率也存在，即
，
.
故和的方程可分别表示为：
∵原点到和的距离相等. ∴
，解得：
或
.
因此
或
.
23．解：（1）采用“代点法”，将O（0，0）代入
中得C=0，A、B不同为零.
（2）直线
与坐标轴都相交，说明横纵截距
均存在.设
，得
；
设
，得
均成立，因此系数A、B应均不为零.
（3）直线只与x轴相交，就是指与y轴不相交——平行、重合均可。因此直线方程将化成
的形式，故
且
为所求.
（4）x轴的方程为，直线方程中
即可.注意B可以不为1，即
也可以等价转化为.
（5）运用“代点法”. 
在直线上，
满足方程， 即
，
故可化为
，
即
，得证.