高一数学第一学期第一次月考试卷
时间：90分钟 满分：100分
一、选择题：本大题共12小题，每小题4分，共48分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．对于关系①∈{x½x≤3，x∈R}；②∈Q；③0ÏN；④0∈Z。其中正确的个数是（ ）
| A. 1 | B. 2 | C. 3 | D. 4 |
2．设集合A=｛1,2｝，B=｛1,2,3｝,C=｛2,3,4｝则
( )
| A. ｛1,2,3｝ | B. ｛1,2,4｝ | C. ｛2,3,4｝ | D. ｛1,2,3,4｝ |
3．已知
则
( )
| A.{x½－3≤x＜－2，或1＜x≤2} | B. {x½－3＜x≤－2，或1＜x} |
| C. {x½－3＜x≤－2，或1≤x＜2} | D. {x½x＜≤―3，或1＜x≤2} |
4．不等式
的解集是 （ ）
A．
B．
C．
D．
5．如图U是全集，M、P、S是U的子集，则图中阴影部分表示的集合是 ( )
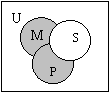A．(M∪P)
S
B．(MP)
S
C．(M∪P)(CUS) D．(MP)(CUS)
６．漳州市对市民进行经济普查，在某小区共400户居民中，已购电脑的家庭有358户，
已购私家车的有42户，两者都有的有34户，则该小区还未购买电脑或私家车的家
庭有 ( )
A．0户 B．34户 C．42户 D．358户
7．设A＝{x½½x－½＞}，B＝{x½x＜a}，若BA，则a的取值范围是（ ）
| A. {a½a≥1} | B. {a½a≤1} | C. {a½a≥2} | D. {a½a≤2} |
8．满足条件{1,2,3}
M{1,2,3,4,5,6}的集合M的个数是 （ ）
A．8 B．7 C．6 D．5
9．设全集U＝Z，A＝{x∈Z½x＜1}，B＝{x∈Z½x≤0}，P＝CU A， Q=CU B，则P、Q的关系是（ ）
| A. PQ | B. P＝Q | C. QP | D. P∈Q |
10．不等式
的解集为 （ ）
| A. {x½0＜x＜2} | B. {x½－2＜x＜0，或2＜x＜4} |
| C. {x½－4＜x＜0} | D. {x½－4＜x＜－2，或0＜x＜2} |
11．设集合M={x│x＝＋，k∈Z}，N＝{x│x＝＋，k∈Z }，则（ ）
| A． M＝N | B. MN | C. MN | D. M∩N＝Æ |
12．设P、Q为两个非空实数集合，定义集合P+Q=
，则P+Q中元素的个数是 （
）
A．9 B．8 C．7 D．6
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在答题卡的相应位置。
13．设全集U＝{2，3，a2＋2a－3}，A＝{5，a＋1}，CU A＝{2}，则a＝ 。
14．设集合P＝{(x，y)½y=－x2＋2，x∈R}，Q＝{(x，y)½y=－x＋2，x∈R}，那么P∩Q＝ 。
15．用列举法表示集合A＝{x½∈N，x∈N }＝ 。
16．二次函数y=ax2+bx+c(x∈R)的部分对应值如下表：
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是_______________________。
高一数学第一学期第一次月考试卷
| 题号 | 一 | 二 | 三 | 总分 | |||
| 17 | 18 | 19 | 20 | ||||
| 得分 | |||||||
一、选择题（每小题4分，共48分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本题共4小题，每小题4分，共16分。把答案填在题中横线上）
（13） ，（14） ，
（15） ，（16） 。
三、解答题：本大题共4小题，共36分。解答应写出文字说明，证明过程或演算步骤。
17．(8分)已知集合A={xx2+x-2≤0}，B={x2<x+1≤4}，C={xx2+bx+c>0}，如果A、B、
C满足(AB)C=Æ，(AB)C=R，求b、c.
18．解不等式：(每小题5分，计10分)
①1-2x-x2≤0 ②
19．（10分）已知集合A＝{x½x2－5x＋4＝0}，B＝{x½x2－2ax＋a＋2＝0}，且A∩B＝B，求a的取值集合。
20．（8分）设集合S中的元素为实数，且满足条件：①S内不含1；②若
，则必有
S。
（1）证明：若2S，则S中必存在另外两个元素，并求出这两个元素；
（2）集合S中的元素能否有且只有一个？为什么？
（附加题10分）：
四、已知集合A＝{x½x2－px－2＝0}，B＝{x½x2＋qx＋r＝0}，A∪B＝{－2，1，5}，则由已知条件能否确定p，q，r的值？若能确定，求出其值；若不能确定，请说明理由。
参考答案
一、BDAAC BBCBD CC
二、13：2 14：{(0，2)，(1，1)} 15：{0，1} 16：{x½x＜－2，或x＞3}
三、17。解：A＝{x½－2≤x≤1}，B＝{x½1＜x≤3}，∴A∪B＝{x½－2≤x≤3}
∵(AB)C=Æ，(AB)C=R，∴C＝{x½x＜－2，或x＞3}，∴x2+bx+c＝0的根为－2，3
∴b＝－1，c＝－6
18．①{x½x≤－1－，或x≥－1＋} ②{x½x＜－2，或0＜x＜3}
19．解：A＝{1，4}，∵A∩B＝B，∴BÍA。
（1）当B＝Æ时，△＝4a2－4(a＋2)＜0，解得－1＜a＜2
（2）当B¹Æ时，△≥0。若△＝0，则a＝－1或a＝2，∴B＝{－1}或B＝{2},不满足。
若△＞0，要使 BÍA，则B＝A，∴，矛盾。
综上，a的取值集合是{a½－1＜a＜2}
20．解：（1）∵2∈S，∴∈S,即－1∈S，∴∈S，即∈S
（2）假设S中只有一个元素，则有a＝，∴a2－a＋1＝0，此方程无实数解。
∴集合S中不能只有一个元素。
四、解：设方程 x2－px－2＝0及x2＋qx＋r＝0的两根分别为x1，x2及x3，x4，由韦达定理得
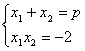及∵A∪B＝{－2，1，5}，∴x1，x2，x3，x4有且仅有两个元素相同，且它们是－2，1，5中得某一个。又由x1x2＝－2，可知或，∴p＝－1。
∴A＝{－2，1}，∴5∈B。x3，x4中另一个应是5或－2或1。
（1） 若B＝{5},则x3＝x4＝5，∴q＝－10，r＝25；
（2） 若B＝{－2，5}，则q＝－3，r＝－10；
（3） 若B＝{1,5},则q＝－6，r＝5。
综上，p，q，r得值可以确定；p＝－1，q＝－10，r＝25；或p＝－1，q＝－3，r＝－10；或
p＝－1，q＝－6，r＝5。