高一数学第一学期期中测试卷
（考试时间90分钟 总分100分）
一. 选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合要求的. ）
1. 已知全集
，
，
，则集合
等于
（ ）
A. 
B.
C. 
D. 
2. 在函数
，
，
，
中，幂函数有
（ ）
A. 0个 B. 1个 C. 2个 D. 3个
3. 已知
，则
的值等于
（ ）
A. 2 B. 3 C. 4 D. 5
4. 满足条件
的集合的个数是
（ ）
A. 1 B. 2 C. 3 D. 4
5. 已知
，
，下列对应法则中，不表示从
的映射的是
（ ）
A. 
B.
C. 
D.
6. 设
，则
、
、
的大小关系是
（ ）
A. 
B.
C. 
D.
7. 函数
的定义域为
（ ）
A. 
B.
C.
D.
8. 要得到函数
的图象只要将函数
的图象 （ ）
A. 作关于
的对称图形 B.
向左平移2个单位
C. 向右平移2个单位 D.
作关于
轴的对称图形
9. 下列函数中，值域是
的函数是
（ ）
A. 
B.
C. 
D.
10. 定义域为
的函数
是偶函数且在
上是增函数，在
上是减函数，又
，则
（ ）
A. 在
上是增函数且最大值是6
B. 在上是减函数且最大值是6
C. 在上是增函数且最小值是6
D. 在
上是减函数且最小值是6
11. 方程
的实数解落在的区间是
（ ）
A. 
B.
C.
D.
12. 设函数
的定义域是
，
，则的值域中所含整数的个数是
（ ）
A. 1个 B.
2个 C.
3个 D.
个
二. 填空题（本题共4小题，每小题4分，共16分. ）
13. 设集合
，
，且
，则
14. 若函数
是偶函数，则的递减区间是
15. 已知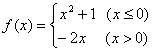
，若
，则
16. 函数是定义在
上的减函数，奇函数，且
，则实数
的取值范围
.
三. 解答题（本小题共5小题，共48分，解答应写出文字说明，证明过程或演算步骤。）
17. （本题满分8分）已知
，
，试用区间表示、.
18. （本题满分10分）已知函数
（
），（1）用分段函数的形式表示该函数；（2）画出该函数的图象；（3）写出该函数的值域、单调区间.
19. （本题满分10分）某学生在体育训练时受了伤，医生给他服用消炎药，现知该药片含药量为200毫克，他的肾脏每天可从体内滤出这种药的60%，
（1）试写出体内残留的药量与经过天数之间的函数关系式；（
）
（2）经过多少天，该同学所服的第一片药在他体内残留不超过10毫克？
20. （本题满分10分）已知函数
（
，
），求（1）的定义域；（2）判断的奇偶性，并给予证明；（3）求使
的
的取值范围.
21. （本题满分10分）已知函数
是奇函数，且
，（1）求函数的解析式；（2）讨论函数在
上的单调性，并加以证明.
【试题答案】
一. 选择题：（本大题共12小题，每小题3分，共36分. 在每小题给出的四个选项中，只有一项是符合要求的。）
（1）D （2）C （3）D （4）B （5）C （6）B
（7）C （8）B （9）A （10）B （11）C （12）D
二. 填空题：（本题共4小题，每小题4分，共16分。）
（13）8；（14）
；（15）
；（16）
三. 解答题：（本小题共5小题，共48分，解答应写出文字说明，证明过程或演算步骤。）
（17）解：集合A表示
的定义域；
由
………………………………………… 3’
集合
表示
的值域；
则
………………………………………… 6’
，
…… 8’
（18）解：（1）
… 3’
（2）如图；……………………………………… 6’
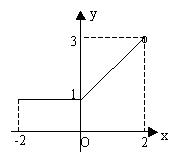
（3）由图可知：值域为
；单调增区间是
…………………… 10’
（19）（1）设经过天之后，体内残余的药量为毫克，
（
）………………… 4’
（2）由
……………………………………………………… 6’
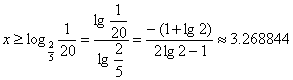……………………… 9’
经过4天，该同学所服的药在他体内残留不超过10毫克………… 10’
（20）（1）由
得
则定义域为
………………………………………………………… 3’
（2）
是奇函数………………………………………………………… 6’
（3）㈠当
时，由
得
，解得
………………………………………… 8’
㈡当
时，由得
，解得
…………………………………………………………… 10’
（21）（1）
是奇函数，
对于一切有意义恒成立
得
…………………………………………………………………… 2’
又
得
…………………………………………………………………… 4’
（2）设任意
，且
…… 6’
㈠当
时，
，
，
即
在
上是增函数；…………………………………………… 8’
㈡当
时，，，
即
在上是减函数. ………………………………………… 10’