高一（上）数学半期考试试题
（I卷）选择题
一、选择题（每小题5分，共50分）
1、将函数
的图像向右平移1个单位，再向上平移2个单位后所得图像对应的函数为（ ）
A、
B、
C、
D、
2、设A是B的充分不必要条件，则非A是非B的（ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
3、函数
的定义域为（ ）
A、
B、
C、
D、
4、若函数
，则
的值为（ ）
A、
B、
C、2 D、
5、若集合
则
=（ ）
A、
B、
C、
D、
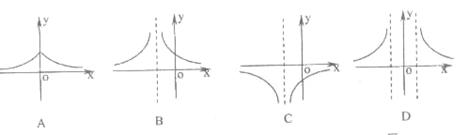
6、函数
的大致图像为（ ）
7、在以下几个说法中，⑴y轴所表示的函数表达式是
；⑵
是定义域为空集的函数；⑶设f是从集合A到集合B的映射，则A中每一个元素在B中都有象；⑷设f是从集合A到集合B的映射，则B为A中元素的象的集合，正确说法的个数有（ ）
A、1个 B、2个 C、3个 D、4个
8、对于任意的
，函数
的值总是大于零，则实数
的取值范围是（ ）
A、
B、
C、
D、
9、定义两种运算：
，则函数
为（ ）
A、奇函数 B、偶函数 C、奇函数且为偶函数 D、非奇函数且非偶函数
10、已知：
，
，在平面直角坐标系
中，函数
的图像与轴交于A点，它的反函数
的图像与
轴交于B点，且这两个函数的图象交于P点，已知四边形OAPB的面积为3，则K值是（ ）
A、3 B、
C、
D、
（II卷）非选择题
二、填空题（每小题4分，共24分）
11、若
，则方程
的根是
12、定义
，若
，则
13、对于定义在R上的函数
，若实数
满足
，则称是函数的一个不动点，若二次函数
没有不动点，则实数
的取值范围是
14、若
是偶函数，则
从小到大的顺序是
15、设
在
上的最大值为8，则在区间
上的最小值是
16、设函数的定义域为R，则下列命题中正确的序号是
（1）若为偶函数，则
的图象关于轴对称；
（2）若为偶函数，则的图象关于直线
对称；
（3）若
，则的图像关于轴对称；
（4）函数和
的图象关于直线对称。
三、解答题（共76分）
17、求值（每小题6分，共12分）
（1）
（2）
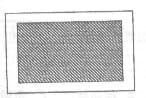18、（12分）要在长为800m，宽为600m的一块长方形地面上进行绿化，要求四周种花卉（花卉的宽度相等），中间阴影部分种草皮（如图），要求草皮的面积不少于总面积的一半，求花卉带宽度的范围。
19、（13分）已知不等式
的解集为A，不等式
的解集为B，其中为实数
（1）当
时，求
（2）若
，求的取值范围。
20、（13分）已知函数
，其中为实数
（1）当
且
时，求的反函数
及其定义域
（2）若
恒成立，求的取值范围。
21、（14分）设函数
，已知满足
的有且只有一个。
（1）求的值；
（2）若函数
，其中
判断并证明
在的单调性；
（3）若存在区间
，使得在上的值域为
，求
的取值范围。
22、（12分）设为实数，记函数
的最大值为
。
（1）设
，求
的取值范围，并把表示为的函数
；
（2）求；
（3）试求满足
的所有实数。