高一(上)数学期末模拟试卷
学校 班级 姓名 得分
一、选择题(每小题3分,共30分)
1、设集合A={3的倍数},B={2的倍数},则A∪B是 ( )
A.{偶数} B.{被2或3整除的数}
C.{6的倍数} D.{2和3的公倍数}
2、已直集合M={yy=x2-1,x∈R},集合N={xy=![]() },则M∩N= ( )
},则M∩N= ( )
A.{(![]() ,1),(
,1),(![]() ,1)}
B.[0,
,1)}
B.[0,![]() ]
]
C.[-1,![]() ]
D.Ф
]
D.Ф
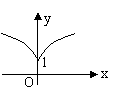
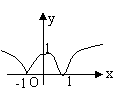
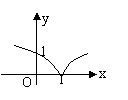
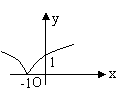 3、函数
3、函数![]() 的图象是
( )
的图象是
( )
A. B. C. D.
4、若![]() <
<![]() ,则x满足
( )
,则x满足
( )
A.x>0 B.x<0 C.x≤0 D.x≥0
5、已知方程x=x+b有一负根,但没有正根,那么 ( )
A.b>0 B.b=0 C. b≥1 D. b<0
6、某商品价降低10%后,欲恢复原价,则应提价 ( )
A.10% B.1%
C.![]() D.
D.![]()
7、半径为3cm的圆中,有一条弧,长度是![]() cm,则此弧所对的圆周角为 ( )
cm,则此弧所对的圆周角为 ( )
A.30° B.15° C.40° D.20°
8、已知O为原点,点A、B的坐标分别是(a,0)、(0,a),其中a>0,点P在线段AB上,
且![]() =
=![]() (0≤t≤1),则
(0≤t≤1),则![]() 的最大值为
( )
的最大值为
( )
A.a B.2a C.3a D.a2
9、使函数![]() 为奇函数,且在[0,
为奇函数,且在[0,![]() ]上是减函数的
]上是减函数的![]() 的一
的一
个值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、已知向量![]() =(
=(![]() ,
,![]() ),
),![]() ,
,![]() =(0,-1),则向量
=(0,-1),则向量![]() 与
与![]() 的夹角
的夹角![]() 为
( )
为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题4分,共20分)
11、若函数![]() 是R上的奇函数,则函数
是R上的奇函数,则函数![]() 图象的对称中心是
。
图象的对称中心是
。
12、函数![]() 的最小值是
。
的最小值是
。
13、关于x的方程![]() 有正根,则实数a的取值范围是
。
有正根,则实数a的取值范围是
。
14、定义一种运算“*”,对于自然数n满足以下性质:
 (1)1*1=1;(2)(n+1)*1=3(n*1)。则n*1用n的代数式表示是
。
(1)1*1=1;(2)(n+1)*1=3(n*1)。则n*1用n的代数式表示是
。
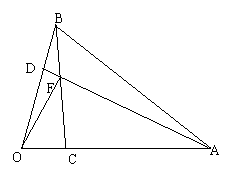
15、如图,三角形OAB中![]() ,
,
![]() , AD、BC交于点F,
, AD、BC交于点F,
设![]() ,
,![]() ,试用
,试用
![]() 、
、![]() 表示
表示![]() 。
。
三、解答题
16、若函数![]() 的定义域为A={xx≥3},值域为B,且A∩B=A,求b的取值范围。(7分)
的定义域为A={xx≥3},值域为B,且A∩B=A,求b的取值范围。(7分)
17、已知关于x的方程![]() 的所有解都大于1,求实数a的取值范围。(7分)
的所有解都大于1,求实数a的取值范围。(7分)
18、已知函数![]() ,
,
(1)求函数的最小正周期T,初相![]() ;
;
(2)当![]() 时,求函数的最大值以及相应的x的取值;
时,求函数的最大值以及相应的x的取值;
(3)求函数的单调递增区间。(9分)
19、如图所示,PQ过三角形OAB的重心G,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
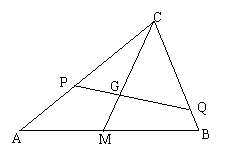 求证:
求证:![]() (7分)
(7分)
20、已知函数![]() ,且
,且![]() ,
,![]() ,
,
(1)求![]() 的最大值与最小值;
的最大值与最小值;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值。(10分)
的值。(10分)
21、已知向量![]() =
=![]() ,
,![]() =
=![]() ,且
,且![]() ,求:
,求:
(1)![]() 及
及![]() ;
;
(2)若![]() 的最小值是
的最小值是![]() ,求实数
,求实数![]() 的值;
的值;
(3)求函数![]() 的最小值。(10分)
的最小值。(10分)
答案:1、B 2、C 3、A 4、B 5、A 6、D 7、B 8、D 9、B 10、A
11、(-2,-1) 12、![]() 13、0<a<1 14、
13、0<a<1 14、![]() 15、
15、![]()
16、b≤2 17、0<a<![]()
18、(1)T=![]() ;
;![]() ,
,
(2)![]() ;
;![]() ,
,
(3)![]()
19、略
20、(1)![]() ;
;![]()
(2)![]() =1
=1
21、(1)![]() =cos2x;
=cos2x;![]() =2cosx
=2cosx
(2)![]() =
=![]()
(3)![]()