高一必修四三角函数单元测试
班级_________学号__________姓名__________
一.选择题:本大题共12小题,每小题5分,共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
1. 化简![]() 等于 ( ) A.
等于 ( ) A. ![]() B.
B. ![]() C. 3 D. 1
C. 3 D. 1
2. 在![]() ABCD中,设
ABCD中,设![]() ,
,![]() ,
,![]() ,
,![]() ,则下列等式中不正确的是( )
,则下列等式中不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 在![]() 中,①sin(A+B)+sinC;②cos(B+C)+cosA;③
中,①sin(A+B)+sinC;②cos(B+C)+cosA;③![]() ;④
;④![]() ,其中恒为定值的是( ) A、① ② B、② ③ C、② ④ D、③ ④
,其中恒为定值的是( ) A、① ② B、② ③ C、② ④ D、③ ④
4. 已知函数f(x)=sin(x+![]() ),g(x)=cos(x-
),g(x)=cos(x-![]() ),则下列结论中正确的是( )
),则下列结论中正确的是( )
A.函数y=f(x)·g(x)的最小正周期为2![]() B.函数y=f(x)·g(x)的最大值为1
B.函数y=f(x)·g(x)的最大值为1
C.将函数y=f(x)的图象向左平移![]() 单位后得g(x)的图象
单位后得g(x)的图象
D.将函数y=f(x)的图象向右平移![]() 单位后得g(x)的图象
单位后得g(x)的图象
5. 下列函数中,最小正周期为![]() ,且图象关于直线
,且图象关于直线![]() 对称的是( )
对称的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 函数![]() 的值域是
( )
的值域是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7. 设![]() 则有( )
则有( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
8. 已知sin![]() ,
,![]() 是第二象限的角,且tan(
是第二象限的角,且tan(![]() )=1,则tan
)=1,则tan![]() 的值为( )
的值为( )
A.-7
B.7
C.-![]() D.
D.![]()
9. 定义在R上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B
B
![]() C
C ![]() D
D
![]()
10. 函数![]() 的周期是( ) A.
的周期是( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
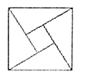 11. 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为
11. 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() 的值等于( )
的值等于( )
A.1 B.![]() C.
C.![]() D.
D.![]()
12. 使函数f(x)=sin(2x+![]() )+
)+![]() 是奇函数,且在[0,
是奇函数,且在[0,![]() ]上是减函数的
]上是减函数的![]() 的一个值( ) A.
的一个值( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题:本大题共4小题,每小题4分,共16分。
13、函数![]() 的最大值是3,则它的最小值______________________
的最大值是3,则它的最小值______________________
14、若![]() ,则
,则![]() 、
、![]() 的关系是____________________
的关系是____________________
15、若函数f(χ)是偶函数,且当χ<0时,有f(χ)=cos3χ+sin2χ,则当χ>0时,f(χ)的表达式为 .
16、给出下列命题:(1)存在实数x,使sinx+cosx=![]() ; (2)若
; (2)若![]() 是锐角△
是锐角△![]() 的内角,则
的内角,则![]() >
>![]() ; (3)函数y=sin(
; (3)函数y=sin(![]() x-
x-![]() )是偶函数; (4)函数y=sin2x的图象向右平移
)是偶函数; (4)函数y=sin2x的图象向右平移![]() 个单位,得到y=sin(2x+
个单位,得到y=sin(2x+![]() )的图象.其中正确的命题的序号是
.
)的图象.其中正确的命题的序号是
.
三、解答题(本大题6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17、(12分) 求值: ![]()
18、(12分) 已知<α<π,0<β<,tanα=- ,cos(β-α)= ,求sinβ的值.
19、(12分) 已知函数![]() (1)求它的定义域、值域以及在什么区间上是增函数; (2)判断它的奇偶性;
(3)判断它的周期性。
(1)求它的定义域、值域以及在什么区间上是增函数; (2)判断它的奇偶性;
(3)判断它的周期性。
20、(12分)求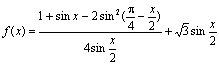 的最大值及取最大值时相应的x的集合.
的最大值及取最大值时相应的x的集合.
21、(12分) 已知定义在R上的函数f(x)=![]() 的周期为
的周期为![]() ,
,
且对一切x![]() R,都有f(x)
R,都有f(x)![]() ;
;
(1)求函数f(x)的表达式; (2)若g(x)=f(![]() ),求函数g(x)的单调增区间;
),求函数g(x)的单调增区间;
22、(14分) 函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)=![]() 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在![]()
高一下期数学(三角函数)测试题 参考答案
一.选择题:本大题共12小题,每小题5分,共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | A | B | B | D | B | D | D | B | B | C | D | B |
1.解;∵![]()
2.解:∵在![]() ABCD中,
ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ∴
∴![]()
3.解:①sin(A+B)+sinC=2sinC;②cos(B+C)+cosA=0;③![]() ;④
;④![]()
4.解:f(x)=sin(x+![]() )
)![]() ,g(x)=cos(x-
,g(x)=cos(x-![]() )
)![]()
5.解:∵最小正周期为![]() ,∴
,∴![]() 又∵图象关于直线
又∵图象关于直线![]() 对称 ∴
对称 ∴![]()
6.解:∵![]() 且
且![]() ∴
∴![]()
7.解:![]()
![]() >
>![]() >
>![]() >
>![]()
8.解:∵![]() ,
,![]() 是第二象限的角,∴
是第二象限的角,∴![]() ,又∵
,又∵![]()
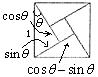 ∴
∴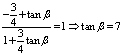 9.解:由已知得:
9.解:由已知得:![]()
10.解: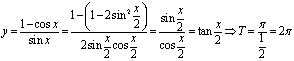
11.解:∵![]() ,又
,又![]() ∴
∴![]()
![]() , ∴
, ∴![]()
![]()
![]()
12.解:∵f(x)=sin(2x+![]() )+
)+![]() 是奇函数,∴f(x)=0知A、C错误;又∵f(x)在[0,
是奇函数,∴f(x)=0知A、C错误;又∵f(x)在[0,![]() ]上是减函数 ∴当
]上是减函数 ∴当![]() 时f(x)=-sin2x成立。
时f(x)=-sin2x成立。
二.填空题:本大题共4小题,每小题4分,共16分。
13、解:∵函数![]() 的最大值是3,∴
的最大值是3,∴![]() ,
,![]()
14、解:∵![]() ∴
∴![]() 、
、![]() 的关系是:
的关系是: ![]() ⊥
⊥![]()
15、∵函数f(χ)是偶函数,且当χ<0时,有f(χ)=cos3χ+sin2χ,则当χ>0时,f(χ)的表达式为:![]()
16、解:(1) ![]() 成立; (2)锐角△
成立; (2)锐角△![]() 中
中![]()
![]() 成立 (3)
成立 (3) ![]()
![]() 是偶函数成立;(4)
是偶函数成立;(4)
![]() 的图象右移
的图象右移![]() 个单位为
个单位为![]() ,与y=sin(2x+
,与y=sin(2x+![]() )的图象不同;故其中正确的命题的序号是:(1)、(2)、(3)
)的图象不同;故其中正确的命题的序号是:(1)、(2)、(3)
三.解答题
17、解: 原式=![]()
![]()
![]()
18、解:∵![]() 且
且![]() ∴
∴![]() ;∵
;∵![]() ,
,![]()
∴![]() ,
,![]() 又∵
又∵![]() ∴
∴![]()
∴![]()
19、解:(1)①∵![]() ∴
∴![]() ,
, ![]()
∴![]() 定义域为
定义域为![]() ②∵
②∵![]() 时,
时,![]()
∴![]() ∴
∴![]() 即
即![]() 值域为
值域为![]() ③设
③设![]() ,
,![]() 则
则![]() ;∵
;∵![]() 单减 ∴为使
单减 ∴为使![]() 单增,则只需取
单增,则只需取![]() ,
,![]() 的单减区间,∴
的单减区间,∴![]() 故
故![]() 在
在![]() 上是增函数。
上是增函数。
(2)∵![]() 定义域为
定义域为![]() 不关于原点对称,
不关于原点对称,
∴![]() 既不是奇函数也不是偶函数。
既不是奇函数也不是偶函数。
(3)∵![]() ∴
∴![]() 是周期函数,周期
是周期函数,周期![]()
20、解:∵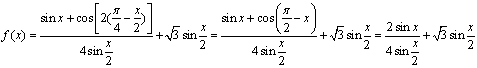
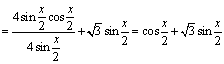
![]()
∴由![]() 得
得![]() 即
即![]() 时,
时,![]() .
.
故![]() 取得最大值时x的集合为:
取得最大值时x的集合为:![]()
21、解:(1)∵![]() ,又周期
,又周期![]() ∴
∴![]()
∵对一切x![]() R,都有f(x)
R,都有f(x)![]() ∴
∴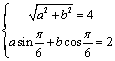 解得:
解得:![]()
∴![]() 的解析式为
的解析式为![]()
(2) ∵![]()
∴g(x)的增区间是函数y=sin![]() 的减区间 ∴由
的减区间 ∴由![]() 得g(x)的增区间为
得g(x)的增区间为![]()
![]() (等价于
(等价于![]()
22、解:① ∵![]() ∴
∴![]() 的定义域为
的定义域为![]()
② ∵![]() ∴f(x)为偶函数;
∴f(x)为偶函数;
③ ∵f(x+![]() )=f(x), ∴f(x)是周期为
)=f(x), ∴f(x)是周期为![]() 的周期函数;
的周期函数;
④ ∵![]()
∴当![]() 时
时![]() ;当
;当![]() 时
时![]()
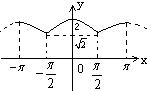 (或当
(或当![]() 时f(x)=
时f(x)=![]()
∴当![]() 时
时![]() 单减;当
单减;当![]() 时
时![]() 单增;
单增;
又∵![]() 是周期为
是周期为![]() 的偶函数
的偶函数
∴f(x)的单调性为:在![]() 上单增,在
上单增,在![]() 上单减。
上单减。
⑤ ∵当![]() 时
时![]() ;当
;当![]() 时
时![]()
∴![]() 的值域为:
的值域为:![]() ⑥由以上性质可得:
⑥由以上性质可得:![]() 在
在![]() 上的图象如上图所示:
上的图象如上图所示: