高一级函数单元检测题
(§2.1----§2.4)
班级: 姓名: 成绩:
一、选择题:(每小题只有一个正确答案,5分×12=60分)
1.下列函数中,在区间(0,2)上为增函数的是( )
A.y=-x+1 B.y=![]() C.y=x2-4x+5 D.y=
C.y=x2-4x+5 D.y=![]()
2.下列各组函数:
①![]() ,
,![]() ;②
;②![]() ,
,![]() ;
;
③![]() ,
,![]() ;④
;④![]() ,
,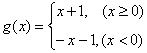 .
.
其中f(x)和g(x)表示同一个函数的是 ( )
A.① B.①和② C.③ D.④
3.设一元二次方程![]() 的根的判别式
的根的判别式![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.R B.![]() C.
C.![]() D.
D.![]()
4. 函数 ![]() 的值域是( )
的值域是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5. “![]() ”是“函数
”是“函数![]() 在区间[1, +∞)上为增函数”的(
)
在区间[1, +∞)上为增函数”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.为确保信息安全,信息需加密传输,发送方由明文![]() 密文(加密),接收方由密文
密文(加密),接收方由密文![]() 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() 例如,明文
例如,明文![]() 对应密文
对应密文![]() 当接收方收到密文
当接收方收到密文![]() 时,则解密得到的明文为( )
时,则解密得到的明文为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知函数f(x)=![]() 的定义域是R,则实数a的取值范围是( )
的定义域是R,则实数a的取值范围是( )
A.a>![]() B.-12<a≤0 C.-12<a<0 D.a≤
B.-12<a≤0 C.-12<a<0 D.a≤![]()
8.函数![]() 的反函数是( )
的反函数是( )
A.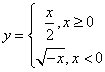 B.
B.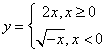 C.
C.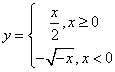 D.
D.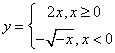
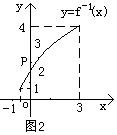 9.函数
9.函数![]() 的反函数
的反函数![]() 的图象与y轴交于点
的图象与y轴交于点
![]() (如图2所示),则方程
(如图2所示),则方程![]() 的根是
的根是![]() ( )
( )
A. 4 B. 3 C. 2 D.1
10.已知函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 的反
函数的图象一定过点( )
的反
函数的图象一定过点( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
11.设函数f(x)=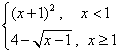 ,则使得f(x)≥1的自变量x的取值范围为( )
,则使得f(x)≥1的自变量x的取值范围为( )
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
12.已知函数![]() 若
若![]() 则 ( )
则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 与
与![]() 的大小不能确定
的大小不能确定
二、填空题:(将正确答案填在题后的横线上,4分×4=16分)
13.已知![]() 的定义域是[1,2],则
的定义域是[1,2],则![]() 的定义域是
.
的定义域是
.
14.已知函数![]() 的反函数为____
______.
的反函数为____
______.
15.已知![]() ,则
,则![]() .
.
16.函数![]() 的单调递增区间是
.
的单调递增区间是
.
三、解答题(共74分)
17.如果二次函数f(x)=![]() 在区间(
在区间(![]() ,1)上是增函数,求f(2)的取值范围。(12分)
,1)上是增函数,求f(2)的取值范围。(12分)
18.若函数f(x)=![]() 的值域为[-1,5],求实数
的值域为[-1,5],求实数![]() 的值。(12分)
的值。(12分)
19.讨论函数f(x)=![]() (a>0)在x∈(-1,1)上的单调性。(12分)
(a>0)在x∈(-1,1)上的单调性。(12分)
20.已知函数![]() ,(1) 当
,(1) 当![]() 时,求函数的值域
时,求函数的值域
(2)求实数![]() ,使得当
,使得当![]() 时,
时,![]() 的值域为
的值域为![]() 。(12分)
。(12分)
21.定义在R上的函数![]() ,当
,当![]() 时,
时,![]() ,且对任意的
,且对任意的![]() ,有
,有![]() 。(14分)
。(14分)
(1)求证:f(0)=1; (2)求证:对任意的x∈R,恒有f(x)>0;
(3)求证:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
22..对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数![]() .(14分)
.(14分)
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
答案:1-----12:BADCA BBCCA AB
13.[0,1];14.![]() ;15.
;15.![]() ;16.(0,1),(1,+∞)
;16.(0,1),(1,+∞)
17.解:对称轴![]() ,由已知得:
,由已知得:![]() ,
,![]()
![]()
![]() ,
,![]()
18.解:由y=f(x)=![]() ,得x2y-ax+cy-1=0.
,得x2y-ax+cy-1=0.
当y=0时,ax=-1,∴a≠0.
当y≠0时,∵x∈R,∴Δ=a2-4y(cy-1)≥0.
∴4cy2-4y-a2≤0.∵-1≤y≤5,∴-1、5是方程4cy2-4y-a2=0的两根.
∴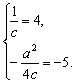 ∴
∴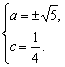
19.解:设-1<x1<x2<1,
则f(x1)-f(x2)=![]() -
-![]()
=![]() =
=![]() .
.
∵-1<x1<x2<1,∴x2-x1>0,x1x2+1>0,(x12-1)(x22-1)>0.又a>0,∴f(x1)-f(x2)>0,函数f(x)在(-1,1)上为减函数.
20.(1)![]() (2)提示:
(2)提示:![]() ,值域
,值域![]() ,所以
,所以![]() 在
在![]() 上单调递增。
上单调递增。![]()
21.(1)证明:令a=b=0,则f(0)=f 2(0).
又f(0)≠0,∴f(0)=1.
(2)证明:当x<0时,-x>0,
∴f(0)=f(x)·f(-x)=1.
∴f(-x)=![]() >0.又x≥0时f(x)≥1>0,
>0.又x≥0时f(x)≥1>0,
∴x∈R时,恒有f(x)>0.
(3)证明:设x1<x2,则x2-x1>0.
∴f(x2)=f(x2-x1+x1)=f(x2-x1)·f(x1).
∵x2-x1>0,∴f(x2-x1)>1.
又f(x1)>0,∴f(x2-x1)·f(x1)>f(x1).
∴f(x2)>f(x1).∴f(x)是R上的增函数.
(4)解:由f(x)·f(2x-x2)>1,f(0)=1得f(3x-x2)>f(0).又f(x)是R上的增函数,
∴3x-x2>0.∴0<x<3.
22.(1)当a=1,b=-2时,f(x)=x2-x-3=x![]() x2-2x-3=0
x2-2x-3=0![]() (x-3)(x+1)=0
(x-3)(x+1)=0![]() x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
x=3或x=-1,∴f(x)的不动点为x=3或x=-1.
(2)对任意实数b,f(x)恒有两个相异不动点![]() 对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根
对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根![]() 对任意实数b,Δ=b2-4a(b-1)>0恒成立
对任意实数b,Δ=b2-4a(b-1)>0恒成立![]() 对任意实数b,b2-4ab+4a>0恒成立
对任意实数b,b2-4ab+4a>0恒成立![]() Δ′=16a2-16a<0
Δ′=16a2-16a<0![]() 0<a<1.
0<a<1.