高一级数学第一学期期中考试
试 题
限时:120分钟
本试卷分第Ⅰ卷和第Ⅱ卷(解答题)两部分,共150分
第Ⅰ卷
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1.在下列关系中,① 0∈{xx2=0}, ② Φ![]() {0,1}, ③ {0,1}={1,0}, ④ {1}
{0,1}, ③ {0,1}={1,0}, ④ {1}![]() {xx2=x}, 其中正确的个数为
( D )
{xx2=x}, 其中正确的个数为
( D )
A.1个 B.2个 C.3个 D.4个
2.设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( D )
A、{1,2} B、{1,5} C、{2,5} D、{1,2,5}
3.下列函数中与函数![]() 相等的是
( C
).
相等的是
( C
).
A.![]() B.
B. ![]() C.
C.![]() D.
D. 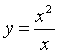
4.已知![]() ,则
,则![]() 的值为
( A )
的值为
( A )
A.1 B.-7 C.-1 D.7
5.下列各式错误的是 ( C ).
A. ![]() B.
B. ![]()
C.
![]() D.
D. ![]()
6.下列函数中为偶函数的是 ( D )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 对于定义在R上的奇函数f(x),下列结论不成立的是 ( B )
A. f(x)![]() f(-x)≤0 B. f(x)-f(-x)=0
f(-x)≤0 B. f(x)-f(-x)=0
C. f(0)=0 D. f(x)=- f(-x)
8.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ( C )
A、1.2 B、1.3 C、1.4 D、1.5
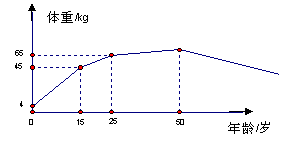 9.下图表示某人的体重与年龄的关系,则
( D )
9.下图表示某人的体重与年龄的关系,则
( D )
A. 体重随年龄的增长而增加
B. 25岁之后体重不变
C. 体重增加最快的是15岁至25岁
D. 体重增加最快的是15岁之前
10.有以下命题:
(1)若函数f(x),g(x)在R上是增函数,则f(x)+g(x)在R上也是增函数;
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则g(x)-f(x)在R上是减函数;
(3)若函数f(x)在区间[1,5]上递增,在(5,9)上也递增,则f(x)在![]() 上递增;
上递增;
(4)若偶函数f(x)在![]() 上递减,则f(x)在
上递减,则f(x)在![]() 上递减。
上递减。
其中正确命题的个数为 ( B )
A.1 B.2 C.3 D.4
二、填空题(本大题共4小题,每小题5分,共20分)
11.![]() 16
。
16
。
12.已知幂函数![]() 的图象过点
的图象过点![]() ,则此幂函数的解析式为
,则此幂函数的解析式为 ![]() ,
,![]() 2 。
2 。
13. 函数![]() 的反函数为
的反函数为 ![]() ;
;
14. 已知函数f(x)=4x2-kx-8在区间![]() 上为减函数,则实数k的取值范围是
上为减函数,则实数k的取值范围是
![]()
高一级数学第一学期期中考试答题卡
一、选择题答案(50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | D | C | A | C | D | B | C | D | B |
二、填空题答案(20分)
11、
16 ; 12、![]() , 2
, 2
13、 ![]() ; 14、
; 14、
![]()
第![]() 卷(解答题部分)
卷(解答题部分)
三、解答题:(本大题6小题,共80分.解答应写出文字说明,证明过程或演算步骤)
15.(本题满分12分)设全集为R,![]() ,
,![]() ,求
,求![]() 及
及![]()
解: ![]() =
=![]() 1分
1分
![]() 3分
3分
![]() 6分
6分
![]() 9分
9分
![]() 12分
12分
16.(本题满分12分)计算:
(1)![]() (2)
(2)![]()
解:
(1)![]() =
=![]() 3分
3分
=![]()
=![]() 6分
6分
(2)![]() =
=![]() 2分
2分
=![]() 4分
4分
=![]() 6分
6分
17. (本题满分12分)求下列函数的定义域
(1)![]() (2)
(2)![]()
解:(1)要使根式![]() 有意义得:
有意义得:![]() , 2分
, 2分
即 ![]() =
=![]()
因为以![]() 为底的指数函数是减函数
为底的指数函数是减函数
![]() 5分
5分
所以 ![]() 6分
6分
(2)要使分式![]() 有意义的实数x的集合是
有意义的实数x的集合是![]() 1分
1分
要使根式![]() 有意义得:
有意义得:![]() 2分
2分
即![]()
不等式的解集是![]() 4分
4分
所以 ![]() =
=![]() 6分
6分
18.(本题满分13分)高明旅社有100张普通客床,若每床每夜收租费10元时,客床可以全部租出;若每床每夜收费提高1`元,便减少5张客床租出;若再提高1元,便再减少5张客床租出。依此情况变化下去。为了获租金最多,每床每夜应提高租金多少元?
解:设每床每夜提高租金x`元,则可租出(100-5x)张床,设可获利润y元,3分
依题意有 ![]()
![]() 8分
8分
即 ![]()
![]()
![]()
![]()
当x=5时 ![]() 12分
12分
答:为了获租金最多,每床每夜应提高租金5元 13分
19.(本题满分15分)已知函数![]() ,
,
(1)判断函数的单调性,并证明你的结论;
(2)求函数的最大值和最小值。
解:(1)函数是减函数
证明:设x1,x2是区间[2,6]上的任意两个实数,且x1<x2,则 1分
![]() 3分
3分
![]() 5分
5分
![]() 6分
6分
![]() 8分
8分
于是![]() 9分
9分
所以,函数![]() 是区间[2,6]上的减函数
10分
是区间[2,6]上的减函数
10分
(2)由(1)可知函数![]() 是区间[2,6]的两个端点上分别取得最大值和最小值,即在x=2时取得最大值,最大值是2,在x=6时取得最小值,最小值是0.4
15分
是区间[2,6]的两个端点上分别取得最大值和最小值,即在x=2时取得最大值,最大值是2,在x=6时取得最小值,最小值是0.4
15分
20.(本题满分16分)已知函数![]() ,函数
,函数![]()
(1)证明:![]()
(2)探究函数![]() 的单调性;
的单调性;
(3)当![]() 时,是否存在实数
时,是否存在实数![]() 使函数
使函数![]() 为奇函数?
为奇函数?
解:(1)![]() 2
2
又![]()
![]() 4分
4分
(2)当![]() 时,
时,![]() 在定义域内是增函数,
在定义域内是增函数,![]() `在定义域内是增函数
7分
`在定义域内是增函数
7分
当![]() 时,
时,![]() 在定义域内是减函数,
在定义域内是减函数,![]() `在定义域内是减函数
10分
`在定义域内是减函数
10分
(3)![]()
由 ![]()
得 ![]() ,
13分
,
13分
![]()
所以,b=1 15分
答:当![]() 时,存在实数b=1,使函数
时,存在实数b=1,使函数![]() 为奇函数 16分
为奇函数 16分