人教(A)版高一立体几何阶段考试
总分150分
一．选择题：（１２*５＝６０）
１．设有两条直线a、b和两个平面
、
，则下列命题中错误的是
（
）
A．若
，且
，则
或
B．若，且
，则
C．若，且，则 D．若
，且，则
２.有一个几何体的三视图如下图所示，这个几何体应是一个( )
（A）棱台 （B）棱锥 （C）棱柱 （D）都不对
３、正三棱锥
的侧棱长和底面边长相等，
如果E、F分别为SC，AB的中点，
那么异面直线EF与SA所成角为 （ ）
A．
B．
C．
D．
|
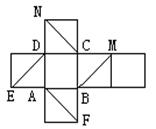
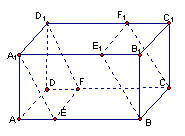
①BM与DE平行；
②CN与BE是异面直线；
③CN与BM成60°角
④DM与BN垂直
以上四个命题中，正确的是 （ ）
A．①②③ B．②④ C．②③④ D.③④
D．③④
５、一个水平放置的平面图形的斜二测直观图是一个底角为
，
腰和上底边均为1的等腰梯形，则这个平面图形的面积是 （ ）
A. 
B. 
C. 
D. 
６、给出下列关于互不相同的直线
和平面
的四个命题:
（1）
则
与m不共面；（2）、m是异面直线，
；（3）若
；（4）若
，则
，其中为错误的命题是 （ ）个.
Ａ．１个 Ｂ．２个 Ｃ．３个 Ｄ．４个
７、设a、b是两条不同的直线，
、
是两个不同的平面，则下列四个命题：
①
若
，
，
，则
；②若
, 
，则
；
③若，，则或
；④若，，
，则
其中正确命题的个数为 A．0 B．1 C．2 D．3 ( )
８. 定点P不在△ABC所在平面内，过P作平面α，使△ABC的三个顶点到α的距离相等，这样的平面共有（ ）（Ａ）１个 （Ｂ）２个 （Ｃ）３个 （Ｄ）４个
９、下列各图是正方体或正四面体，P，Q，R，S分别是所在棱的中点，这四个点中不共面的一个图是
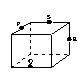
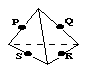
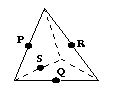
（A） （B） （C） （D）
１０、如图，在一根长11cm，外圆周长6cm的圆柱形柱体外表面，用一根细铁丝缠绕，组成10个螺旋，如果铁丝的两端恰好落在圆柱的同一条母线上，则铁丝长度的最小值为
（A） 61cm （B）
cm
（C）
cm （D）10
cm
|
中，
，分别过BC、
的两个平行截面将长方体分成三部分，
其体积分别记为
，
。
若
，则截面
的面积为
(A)
(B)
(C)
(D)
１２. 已知球的两个平行截面的面积分别为5π和8π，它们位于球心的
同一侧且相距是1，那么这个球的半径是( )
A.4 B.3 C.2 D.5
二．填空题：（４*６＝２４）
１３ 已知ａ、ｂ为不垂直的异面直线，α是一个平面，则ａ、ｂ在α上的射影有可能是.①两条平行直线 ②两条互相垂直的直线 ③同一条直线 ④一条直线及其外一点在一面结论中，正确结论的编号是 (写出所有正确结论的编号).
１４．【06山东·理】如图，在等腰梯形ABCD中，AB=2DC=2，∠DAB=60°，E为AB的
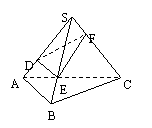中点，将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则三棱锥P－DCE的外接球的体积为＿＿＿＿＿＿＿＿＿＿
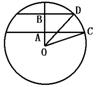
１５如图，一个盛满水的三棱锥容器，不久发现三条侧棱上各有一个小洞
，且知
，若仍用这个个容器盛水，则最多可盛水的体积是原来的＿＿＿＿＿＿＿＿＿
１６. 平面a ∥平面b ，过平面a 、b 外一点P引直线PAB分别交a 、b 于A、B两点，PA=6，AB=2，引直线PCD分别交a 、b 于C、D两点．已知BD=12，则AC的长等于＿＿＿＿＿＿＿
三．解答题：１７.如图，在四面体ABCD中，已知所有棱长都为a，点E、F分别是AB、CD的中点.
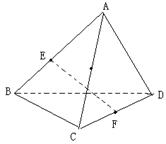（1）求线段EF的长;(EF是两异面直线AB与CD的公垂线)；
（2）求异面直线BC、AD所成角的大小.１２分
１８
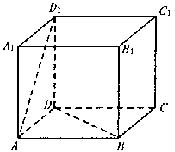
１２分 如图，正方体ABCD—A1B1C1D1的棱长为1，PQ分别是线段AD1和BD上的点，且D1P∶PA=DQ∶QB=5∶12.
 |
(1) 求证PQ∥平面CDD1C1； (2) 求证PQ⊥AD；.
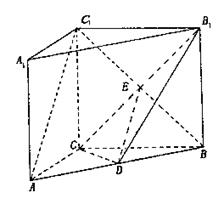
１９ １２分 如图, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AA1＝4，AB=5,点D是AB的中点，
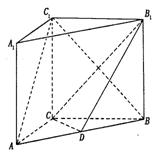（I）求证：AC⊥BC1；（II）求证：AC 1//平面CDB1；
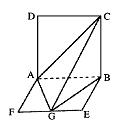２０、如图，平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，且
G是EF的中点，（1）求证平面AGC⊥平面BGC；
（2）求GB与平面AGC所成角的正弦值. .13分
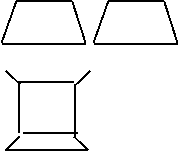
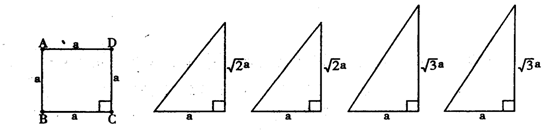
２１.(1３分)如图所示的一组图形为某一四棱锥S—ABCD的侧面与底面，(1)请画出四棱锥S—ABCD的示意图，使SA⊥平面ABCD，并指出各侧棱长；（2）在（1）的条件下，过A且垂直于SC的平面分别交于SB、SC、SD于E、F、G.求证AE⊥平面SBC.
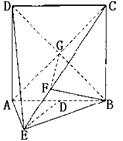
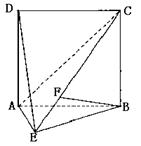２２、（本小题满分1４分）如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.
（Ⅰ）求证AE⊥平面BCE；
（Ⅱ）求二面角B—AC—E的大小； （Ⅲ）求点D到平面ACE的距离.
答案
１－４ ＤAＣＤ ； ５－８BAＤＤ
９－１２ＤＡCB
１３ ①②④ １４．
１５
１６， AC=9．18
１７．１７，（1）连CE、DE，在等边△ABC中，EC=DE=
a，
∴EF是等腰△ECD底边上的高，EF⊥CD，
EF=
=
a
（2）方法一：
取BC中点G，连AG、DG，易知BC⊥AG、BC⊥DG，
∴BC⊥面AGD，则BC⊥AD，∴BC，AD所成角为900，
方法二：
取AC中点H，连EH、FH，则θ=∠EHF是BC、AD所成的角，
由余弦定理得cosθ=
=0，θ=900，
１８．讲解: （1）在平面AD1内，作PP1∥AD与DD1交于点P1，在平面AC内，作
1∥BC交CD于点Q1，连结P1Q1.
∵ 
,
∴PP1
1 .
由四边形P1P1为平行四边形, 知PQ∥P1Q1
而P1Q1
平面CDD1C1， 所以PQ∥平面CDD1C1
（2）
AD⊥平面D1DCC1， ∴AD⊥P1Q1，
又∵PQ∥P1Q1， ∴AD⊥PQ.
１９．解法一：（I）直三棱柱ABC－A1B1C1，底面三边长AC=3，BC=4AB=5，
∴ AC⊥BC，且BC1在平面ABC内的射影为BC，∴ AC⊥BC1；
（II）设CB1与C1B的交点为E，连结DE，∵ D是AB的中点，E是BC1的中点，∴ DE//AC1，
∵
DE
平面CDB1，AC1
平面CDB1，∴ AC1//平面CDB1；
２０．（1）证明：正方形ABCD
∵面ABCD⊥面ABEF且交于AB，
∴CB⊥面ABEF ∵AG，GB面ABEF， ∴CB⊥AG，CB⊥BG
又AD=2a，AF= a，ABEF是矩形，G是EF的中点，
∴AG=BG=
，AB=2a， AB2=AG2+BG2，∴AG⊥BG ∵CG∩BG=B ∴AG⊥平面CBG 而AG面AGC， 故平面AGC⊥平面BGC
（2）解：如图，由（Ⅰ）知面AGC⊥面BGC，且交于GC，在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC， ∴∠BGH是GB与平面AGC所成的角
∴在Rt△CBG中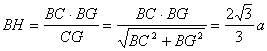
又BG=
，
∴
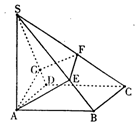２１．（1）画出示意图如右，其中，SA=
（2）∵SC⊥平面AEFG，A又AE平面AEFG，∴AE⊥SC，∵SA⊥平面BD，又BC平面BD，∴SA⊥BC.又AB⊥BC，SA∩AB=A, ∴BC⊥平面SBＡ，∴ ＢＣ┻ＡＥ
∴AE⊥平面SBC，
２２．．解：（Ⅰ）
平面ACE. 
∵二面角D—AB—E为直二面角，且
， 
平面ABE.
…………4分
（Ⅱ）连结BD交AC于C，连结FG，
∵正方形ABCD边长为2，∴BG⊥AC，BG=
，
平面ACE，
由三垂线定理的逆定理得FG⊥AC.
是二面角B—AC—E的平面角. …….6分
由（Ⅰ）AE⊥平面BCE， 又
，
∴在等腰直角三角形AEB中，BE=.
又直角
，
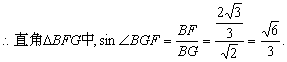
∴二面角B—AC—E等于
………………………………………9分
（Ⅲ）过点E作
交AB于点O. OE=1.
∵二面角D—AB—E为直二面角，∴EO⊥平面ABCD.
设D到平面ACE的距离为h，
平面BCE，
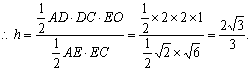
∴点D到平面ACE的距离为
………..12分