高一年级《 数学 》第一学期期终考试试卷
本试卷分卷Ⅰ和卷Ⅱ两部分。卷Ⅰ为选择题，卷Ⅱ为非选择题。
本试卷共150分。考试时间为120分钟。
第Ⅰ卷（选择题，共60分）
一、选择题（每小题5分，共60分）
1、集合P={1，a}，
是集合P中的元素，则a可取值有：
A．0个 B．1个 C．2个 D．3个
2、在等差数列{an}中，公差
的值（ ）
A．
B．
C．
D．1
3、函数
(
)的反函数是：
A．
B．
C．
D．
4、等差数列
中，若
，则
A．45 B．75 C．180 D．320
5、函数
的值域是：
A．
B．[－1，3]
C．[0，3] D．[－1，0]
6、已知数列的通项是
=2n－37，则其前n项和
取最小值时n的值为：
A．16 B．17 C．18 D．19
7、下列各组函数中，表示同一个函数的是（ ）
A．
与
B． 
与
C．
与
D． 
与
（
且
）
8、已知是等比数列，且＞0，
，则
A．5 B．10 C．15 D．20
9、如果函数
对任意实数
，都有
，则：
A．
B．
C．
D．
10、命题甲“
，b，c成等比数列”，命题乙“
”，那么甲是乙的：
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又非必要条件
11、为了得到函数
的图象，可以把函数
的图象（ ）
A． 向左平移3个单位长度 B．向右平移3个单位长度
C． 向左平移1个单位长度 D．向右平移1个单位长度
12、某商品零售价2006年比2005年上涨25%，欲控制2007年比2005年上涨10%，则2007年比2006年应降价 （ ）
A．15% B．12% C．10% D．5%
选择题答题卡：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
第Ⅱ卷（非选择题，共90
分）
二.填空题：（每小题4分，共16分）
13．已知等差数列的公差是正数，且
，
，则
等于 ．
14．一个正项等比数列的前
项和为
，若
，
，则
等于 ．
15．已知
的反函数为
，若的图象经过点Q（5，2），则
等于
．
16.已知函数
满足：对任意实数
，有
，且
，写出一个满足条件的函数，则这个函数可以写为= ．（注：只需写出一个满足条件的函数即可）
三、解答题：
17、（12分） 解不等式
18、（每小题6分，共12分）化简下列各式：
① ㏒
25×㏒
4×㏒
9
②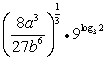 
19、（12分）三个正数成等差数列，它们的和等于15，如果它们分别加上1，3，9就成等比数列，求这三个数。
20、（12分）已知数列的前项和
求的通项公式、首项、公差。
21、（12分）已知二次函数满足条件
和
（1）求的解析式；
（2）求在区间
上的最大值和最小值。
22、（14分）已知数列中
，且
（1）求
；
（2）求数列的通项公式。
答案
一、选择题：共12小题，每小题5分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | C | A | B | C | B | C | D | A | A | D | D | B |
二、填空题：共4小题，每小题4分
13、 ２
14、 ６３ 15、 １ 16、只要满足形式
即可
17、 解：由原不等式得
或
∴ 
或
∴ 
或
∴ 不等式的解集是
１８、解：
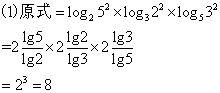
19、解：这三个数依次为：
、
、
20解：
，
，
21、 解： 
（2）最大值3，最小值
22、解：
（1）
，
（2）∵ 
∴ 
