高一年级第一学期期中考试数学试卷
本试卷满分160分，考试时间120分钟
一 选择题 (每题5分,共50分)
1.设集合U=
｛1，2，3，4，5，6，7｝ A=｛2，4，6｝ B=｛1，3，5｝则
（ ）
A.｛1，3，5｝ B. ｛2，4，7｝ C. ｛2，4，6｝ D.｛1，5，7｝
2..函数y=
+
的定义域为
( )
A. （
）
（
，+
） B. R C. （0，）（，+） D（0，+）
3已知集合M=
x︱x＜3
N= x︱
, 则M
N等于 （ ）
A. 
B. x∣0＜x＜3 C x∣1＜x≤3 D x︱
4.下表表示y为x的函数，则函数的值域为 （ ）
| x | -5＜x＜0 | 0≤x＜5 | 5≤x＜10 | 10≤x＜15 | x≥15 |
| y | -1 | 0 | 1 | 2 | 3 |
A. [ -1, 3 ] B.（-5，+） C. ｛-1，0，1，2，3｝ D. N
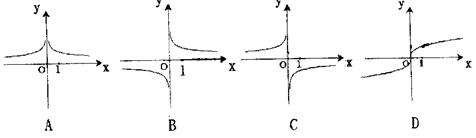
5下列四张图中表示函数
图像的是 （ ）
6.对于二次函数f（x）=a
+bx+c , 对任意实数m都有f（m）=f（4-m）成立， 在函数值f（1），f（-1），f（2），f（5）中最大的一个不可能是 （ ）
A f（-1） B. f（1） C. f（2） D. f（5）
7.某公司在A， B两地销售一种商品，利润分别为
=5.06x-0.15 , 
=2x， 其中x为销售量，若公司在两地共销售15台，则能获得的最大利润为 （
）
A.45.606 B. 45.6 C.45.56 D.45.51
8.设集合M=
N=
, 那么M
N元素的个数为 （ ）
A.0 B. 1 C.2 D. 3
9.在下列区间中方程
-x-3=0必有实数解的是
（ ）
A. [-1， 0] B.[0， 1] C. [1， 2] D.[2， 3]
10下列四个命题正确的个数是 （ ）
（１）定义在Ｒ上的函数g（x），若满足g（-2）=g（2）且 g（-5）=g（5）则g（x）为偶函数 ；
（2）定义在Ｒ上的函数g（x），g（-5）≠g（5） 则g（x）不为偶函数 ；
（3）定义在Ｒ上的函数g（x）在区间(-，0]上增函数，在[0，+)上也是增函数 则函数g（x）在R上为增函数；
（4）定义在Ｒ上的函数 g（x）满足g（2）＞g（1）则函数g（x）在R上不是减函数；
A 1 B 2 C 3 D 4
二 填空题 (每题6分,共36分)
11幂函数y=f（x）图像过点（2，
）,f（9）=
12化简
=
13.奇函数f（x）在区间[-1,1]为增函数,且对任意m有
,则m的取值范围为
14. 函数f（x）=3-ax+4在[5，+] 上为增函数,则a的范围为
15函数
在R上为奇函数, 当
时,
,则当
时,f(x)=
16奇函数f（x）满足f（x+1）=－f（x），当x
（0，1）时,
则
三 解答题（本题共74分）
17. (本题12分) 判断函数
在区间
的单调性并加以证明
18. (本题14分) 已知集合A=
B=
(1)
若AB=B 求实数m的取值范围;
(2) 若AB≠求实数m的取值范围.
19．(本题15分) 已知函数
（1） 求函数f（x）的定义域并判断奇偶性;
（2）
设
，
为定义域内的任意两个值，比较f（）+f（）与f（
）的大小,并证明你的结论;
（3）
设f（
）=1 f（-n）=
求 f（m））
20.(本题16分) 设二次函数g（x）满足g（x）=g（-3-x），g（-2）=11,图象与y轴交点的纵坐标为7
（1） 求二次函数的g（x）表达式
(2)
设f（x）=mx+1当 x[-1，1]时 g（x）＞f（x）恒成立，求m范围
21.(本题17分) 对于定义域为D的函数,若同时满足下列条件:
① 
在D内单调递增或单调递减;
②存在区间
,使在
上的值域为;那么把
叫闭函数.
(1)
判断函数
是否为闭函数; 若是,则求出满足②的区间;
若不是请说明理由;
(2) 若
是闭函数,求实数k的范围.