《解三角形》测试题

数学必修5第一章《解三角形》测试题

班级　　　　　　   姓名 　　　　　　  座号 　　　　　　总分 　　　　　　　　 

一、选择题(本大题共6小题，每小题6分，共36分)

1．已知△ABC中，a＝4，b＝4，∠A＝30°，则∠B等于(　　)

　　A．30°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．30°或150°

　　C．60°　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．60°或120°

2．在△ABC中，若，则与的大小关系为（ 　 ）

A. 　　　B. 　　　 C. ≥　　　 D. 、的大小关系不能确定

3．已知△ABC中，AB＝6，∠A＝30°，∠B＝120°，则△ABC的面积为(　　)

　　A．9　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．18

　　C．9　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．18

4．在△ABC 中，sinA:sinB:sinC=3:2:4，则cosC的值为（　 　 ）

　　A．  　　　　　B．－ 　　　　　 C．　　　　　  D．－

5．关于x的方程有一个根为1，则△ABC一定是（　　 ）

　　　 A. 等腰三角形　　　B. 直角三角形　　　C. 锐角三角形　　　D. 钝角三角形

6. 已知A、B、C是△ABC的三个内角，则在下列各结论中，不正确的为(　　)

　　A．sin²A＝sin²B＋sin²C＋2sinBsinCcos(B＋C)

　　B．sin²B＝sin²A＋sin²C＋2sinAsinCcos(A＋C)

　　C．sin²C＝sin²A＋sin²B-2sinAsinBcosC

　　D．sin²(A＋B)＝sin²A＋sin²B-2sinBsinCcos(A＋B)

二、填空题(本大题共4小题，每小题6分，共24分)

7．一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东，行驶４h后，船到达C处，看到这个灯塔在北偏东，这时船与灯塔的距离为　　　　 km．

8．在△ABC中，若AB＝，AC＝5，且cosC＝，则BC＝________．

9、中，若b=2a , B=A+60°,则A=　　　　 .

10．在△ABC中，∠C＝60°，a、b、c分别为∠A、∠B、.C的对边，则＝________．

三、解答题(本大题共3小题，共40分)

11．(本小题共12分)已知a＝3，c＝2，B＝150°，求边b的长及S_△．

12. (本小题共14分)在ABC中，设，求A的值。

13. (本小题共14分) 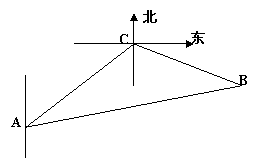一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.

　

　

　　

答案

一DACDAD

二7.　　 8. 4或5　 9.　30°

10 .1

 三

11．解：b²＝a²＋c²-2accosB＝(3)²＋2²-2·3·2·(-)＝49．

　　∴　b＝7，

S_△＝acsinB＝×3×2×＝．

12. 解：根据正弦定理

13.  解:  设A,C分别表示缉私艇,走私船的位置,设经过  小时后在B处追上,　则有

,

所以所需时间2小时,