高一级数学科第二学期期末统一考试
试卷
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页，满分100分，考试时间100分钟。
注意事项：
1．答题前，考生必须将自己的姓名、统考考号、座号和考试科目用铅笔涂写在答题卡上。
2．第I卷共10小题，每小题选出答案后，用铅笔把答题卡上对应的答案标号涂黑，如要改动，必须用橡皮擦干净后，再选涂其他答案。第II卷则用黑色的钢笔（或圆珠笔）按各题要求答在答题卡相应的位置上。
3．不可以使用科学型计算器.
4．考试结束时，将答题卡交回。
第I卷（选择题共40分）
一、选择题（每小题4分，共40分）
1．
=
A．
B．
C．
D．
2．某公司有员工49人，其中30岁以上的员工有14人，没超过30岁的员工有35人，为了解员工的健康情况，用分层抽样的方法抽一个容量为7的样本，其中30岁以上的员工应抽多少
A．2人 B．4人 C．5人 D．1人
3．把21化为二进制数，则此数为
A．10011(2) B．10110(2) C．10101(2) D．11001(2)
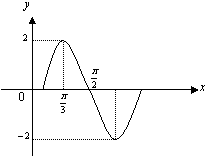4．已知函数
一个周期的图象（如图），则这个函数的一个解析式为
A．
B．
C. 
D．
5．
等于
A．
B．
C．
D．
6．已知
，
，
为非零向量,且·=·，则有
A．=
B．⊥
C．(-)⊥ D．=或(-)⊥
7．下面四个选项中取
的值，使函数
是奇函数，则的取值是
A．
B．
C．
D．
8. 在抽取产品的尺寸过程中，将其尺寸分成若干组，
是其中一组，抽查出的个体在该组上的频率为m ，该组上的直方图的高为h，则
A．hm B．
C．
D．h+m
9. 设
，若
的夹角为
，
的夹角为，且
，则
的值为
A．
B． C． D．1
10．图中所示的是一个算法的流程图，表达式为
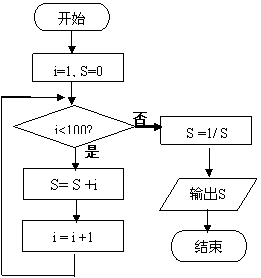A．
B．
C．
D．
第II卷（非选择题共60分）
二、填空题（每小题4分，共16分）
11．某人射击5次，分别为8，7，6，5，9环，这个人射击命中的平均环数为 .
12．已知
，则
的值为
.
13．当
时，则
的概率为 .
14．若
在区间
上的最大值是
，则
=
三、解答题（共5小题. 15、16、17、18题各9分，19题8分，合计44分）
15．（9分）将一枚质地均匀的硬币连续投掷3次，求以下事件的概率；
（1）3次正面向上
（2）2次正面向上，1次反面向上
16．（9分）已知非零向量
，满足
=1且
；
（1）若
，求向量的夹角；
（2）在⑴的条件下，求
的值。
17．（9分）在ΔABC中，
。
（1）求
的值；
（2）求
的值。
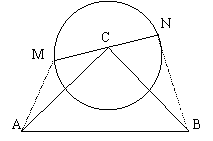
18．（9分）Rt△ABC中，∠C=90°，AC=BC=2，⊙C的半径是1，MN是⊙C直径。求：
·
的最大值及此时
与
的关系.
 |
19．（8分）已知
=（2acosx，b），
=（cosx，sinxcosx）函数f（x）=·，且f（0）=2，
（1）求a，b的值及f（x）的最小值；
（2）若函数
（其中
为常数），求函数
的单调增区间。
高一级数学科第二学期期末统一考试参考答案
一、BACDD DABCA
二、11. 7； 12.
； 13. 
； 14. 
三、
15．解：（1）∵将一枚质地均匀的硬币连续投掷3次的基本事件总数为
；
又事件“3次正面向上”共有基本事件数为1；
设事件“3次正面向上”为A
∴P（A）=
∴事件“3次正面向上”发生的概率为。
（2）又事件“2次正面向上，1次反面向上”共有基本事件数为3；
设事件“2次正面向上，1次反面向上”为B
∴P（B）=
∴事件“2次正面向上，一次反面向上”发生的概率为。
16．解：（1）∵，
∴
即
；
又=1，∴
∵；∴
，
∴
∴向量的夹角为45o
（2）∵
∴
17．解：（1）在ΔABC中, ∵
,
∴
∴
∴
∴
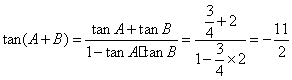
（2）∵
∴
∴
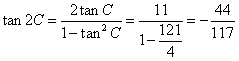
18．解：设
，则
；
·
又∠C=900，所以
·
当
时，·
最大；
此时
∥
即与平行（共线）。
19．解：（1）由题可知f（x）=
=2acos2x+bsinxcosx 进而得
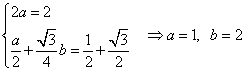
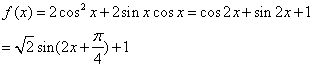
所以，f（x）的最小值为
，此时
。
（2）
①当=0时，函数即不增也不减；
②当>0时，函数的单调递增时，
的单调增区间为
；
③当<0时，函数的单调递增时，
的单调增区间为
综上所述，当=0时，函数即不增也不减；
当>0时，的单调增区间为
当<0时，的单调增区间为