高一数学(必修2)模拟题
一、选择题(本大题共10小题,每小题4分,共40分,将答案直接填在下表中)
(1)下列命题为真命题的是( )
(A)平行于同一平面的两条直线平行 (B)垂直于同一平面的两条直线平行
(C)与某一平面成等角的两条直线平行 (D)垂直于同一直线的两条直线平行
(2)若一个角的两边分别和另一个角的两边平行,那么这两个角( )
(A)相等 (B)互补 (C)相等或互补 (D)无法确定
(3)正三棱锥的底面边长为2,侧面均为直角三角形,则此棱锥的体积为( )
 (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
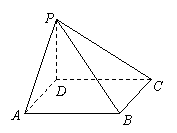
(4)已知PD⊥矩形ABCD所在的平面,图中相互垂直的平面
有( )
(A)2对 (B)3对
(C)4对 (D)5对
(5)如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)如果直线![]() 与直线
与直线![]() 平行,则
平行,则![]() 的值为( )
的值为( )
(A)3 (B)-3 (C)5 (D)0
(7)在空间直角坐标系中点P(1,3,-5)关于![]() 对称的点的坐标是(
)
对称的点的坐标是(
)
(A)(-1,3,-5) (B)(1,-3,5)
(C)(1,3,5) (D)(-1,-3,5)
(8)过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )
(A)4x+3y-13=0 (B)4x-3y-19=0
(C)3x-4y-16=0 (D)3x+4y-8=0
(9)已知点(a,2)(a>0)到直线l:x-y+3=0的距离为1,则a等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1+
(D)1+![]()
(10)若圆![]() ,
,![]() ,则
,则![]() 和
和![]() 的位置关系是(
)
的位置关系是(
)
(A)外离 (B)相交 (C)内切 (D)外切
二、填空题(本大题共6小题,每小题4分,共24分)
(11)底面直径和高都是4cm的圆柱的侧面积为 cm2.
(12)若两个球的表面积之比是4∶9,则它们的体积之比是 .
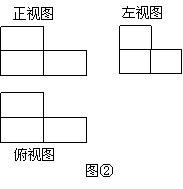
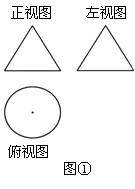
(13)图①中的三视图表示的实物为_____________;
图②为长方体积木块堆成的几何体的三视图,此几何体共由_______块木块堆成.
 | |||
 | |||
(14)直线![]() 的倾斜角的大小为
.
的倾斜角的大小为
.
(15)方程![]() 所确定的直线必经过的定点坐标是 .
所确定的直线必经过的定点坐标是 .
(16)设M是圆![]() 上的点,则M到直线
上的点,则M到直线![]() 的最长距离是
.
的最长距离是
.
三、解答题(本大题共4小题,共36分.解答应写出文字说明、演算步骤或推证过程)
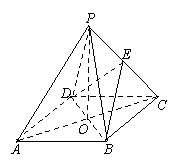 (17)(本小题满分9分)
(17)(本小题满分9分)
如图,O是正方形ABCD的中心,
PO![]() 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC ![]() 平面BDE.
平面BDE.
(18)(本小题满分9分)
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和.
(Ⅰ)求该圆台的母线长;
(Ⅱ)求该圆台的体积.
(19)(本小题满分9分)
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点.
(Ⅰ)求AB边所在的直线方程;
(Ⅱ)求中线AM的长.
(20)(本小题满分9分)
一圆与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,在
上,在![]() 上截得的弦长为
上截得的弦长为![]() ,求此圆的方程.
,求此圆的方程.
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | A | D | A | B | C | A | C | D |
二、填空题
(11)![]() (12)8∶27
(13)圆锥;4
(12)8∶27
(13)圆锥;4
(14)60° (15)(0,3) (16)8
三、解答题
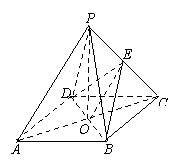 (17) 证明:(Ⅰ)连结EO,
(17) 证明:(Ⅰ)连结EO,
在△PAC中,∵O是AC的中点,E是PC的中点,
∴OE∥AP.
又∵OE![]() 平面BDE,
平面BDE,
PA![]() 平面BDE,
平面BDE,
∴PA∥平面BDE.
(Ⅱ)∵PO![]() 底面ABCD,
底面ABCD,
∴PO![]() BD.
BD.
又∵AC![]() BD,且AC
BD,且AC![]() PO=O,
PO=O,
∴BD![]() 平面PAC.
平面PAC.
而BD![]() 平面BDE,
平面BDE,
∴平面PAC![]() 平面BDE.
平面BDE.
(18)解:(Ⅰ)设圆台的母线长为![]() ,则
,则
圆台的上底面面积为![]() ,
,
圆台的下底面面积为![]() ,
,
所以圆台的底面面积为![]()
又圆台的侧面积![]() ,
,
于是![]() ,即
,即![]() 为所求.
为所求.
(Ⅱ)由(Ⅰ)可求得,圆台的高为![]() .
.
∴ ![]()
=![]()
=![]() .
.
(19) 解:(Ⅰ)由两点式得AB所在直线方程为: ![]() ,
,
即 6x-y+11=0.
另解:直线AB的斜率为:![]() ,
,
直线AB的方程为 ![]() ,
,
即 6x-y+11=0.
(Ⅱ)设M的坐标为(![]() ),则由中点坐标公式得,
),则由中点坐标公式得,
![]() , 即点M的坐标为(1,1).
, 即点M的坐标为(1,1).
故![]() .
.
(20) 解:设所求圆的方程为![]() ,则
,则
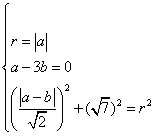 ,
,
解得![]() 或
或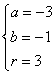 .
.
所以,所求圆的方程为![]() ,或
,或![]() .
.