高一数学第二学期期末考试
试卷
说明:本试卷共三大题22小题,满分150分,考试时间为120分钟.不准用计算器.答案一律做在答题卷上,否则无效.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一个是符合题目要求的。请将所选答案代号填入题后的答题卡中。
1. 已知m =(4,2),n =(x,-3),且m∥n ,则x的值为( )
A.6 B.-6 C.4 D.-4
2. 点![]() 分
分![]() 所成的比为
所成的比为![]() ,则下列结论正确的是 ( )。
,则下列结论正确的是 ( )。
A.点![]() 分
分![]() 的比为
的比为![]() B.点
B.点![]() 分
分![]() 的比为
的比为![]()
C.点![]() 分
分![]() 的比为
的比为![]() D.点
D.点![]() 分
分![]() 的比为
的比为![]()
3.
按向量![]() 将点
将点![]() 平移到点
平移到点![]() ,则按向量
,则按向量![]() 将点
将点![]() 平移到 ( )。
平移到 ( )。
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.
函数![]() 与函数
与函数![]() 的周期之和为
的周期之和为![]() ,则正实数
,则正实数![]() 的
的
值为 ( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.
已知![]() ,则
,则![]() 等于 ( )。
等于 ( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.
已知平行四边形![]() 满足条件
满足条件![]() ,则该四边形是 ( )。
,则该四边形是 ( )。
A.矩形 B.菱形 C.正方形 D.任意平行四边形
7.
已知向量![]() ,若
,若![]() ,则
,则![]() 的值是 ( )。
的值是 ( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.
 与向量
与向量![]() 垂直的单位向量坐标为 ( )
垂直的单位向量坐标为 ( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
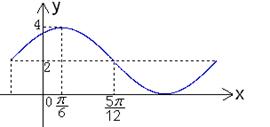
9.
已知函数![]() 的一部分图象如右图所示,如果
的一部分图象如右图所示,如果![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.
角![]() 满足条件
满足条件![]() ,则
,则![]() 在 ( )
在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比为m则m的取值范围是( )
A.(1,2) B.(2,+![]() ) C.[3,+
) C.[3,+![]() ] D.(3,+
] D.(3,+![]() )
)
12.![]() 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且![]() 在区间(0,6)内解的个数的最小值是( )
在区间(0,6)内解的个数的最小值是( )
A.2 B.3 C.4 D.5
二、填空题:(每小题4分,4个小题共计16分)
13.函数![]() 的值域是
。
的值域是
。

![]() 14在
14在![]() 中,已知O是BC的中点,过O的直
中,已知O是BC的中点,过O的直
 线分别交 AB的延长线和AC于点M,N,若
线分别交 AB的延长线和AC于点M,N,若![]() ,
,
![]()
![]() ,则
,则![]() =
。.
=
。.
15.若向量![]() ,且
,且![]() 的夹角为钝角,则
的夹角为钝角,则![]() 的取值范围是________。
的取值范围是________。
16给出下列命题:
①函数![]() 是偶函数; ②函数
是偶函数; ②函数![]() 在闭区间
在闭区间![]() 上是增函数;
上是增函数;
③直线![]() 是函数
是函数![]() 图象的一条对称轴;④将函数
图象的一条对称轴;④将函数![]() 的图象向左平移
的图象向左平移![]() 单位,得到函数
单位,得到函数![]() 的图象;其中正确的命题的序号是
.
的图象;其中正确的命题的序号是
.
高一数学试卷答题卷
一.选择题答题卡:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题 共90分)
二.填空题:本大题共4个小题,每小题4分,共16分。请将答案填在题后的横线上。
13 。 14 。
15 。 16 。
三、解答题:(本大题共6个小题,74分。解答应写出文字说明、证明过程或演算步骤。)
17、(本大题满分12分)已知![]() .
.
(I)求sinx-cosx的值; (Ⅱ)求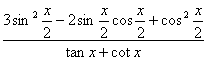 的值.
的值.
18、(本大题满分12分)已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() 求常数
求常数![]() 的值。
的值。
19、(本大题满分12分)已知平面向量a=![]() ,b=
,b=![]() ,若存在实数
,若存在实数![]() 和
和![]() ,使x=a+
,使x=a+![]() b, y=
b, y=![]() a+
a+![]() b,且x
b,且x![]() y,试求函数的关系式
y,试求函数的关系式![]() 。
。
20、(本大题满分12分).已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() 、
、![]() 、
、![]()
(Ⅰ)若![]() 是
是![]() 边上的高,求向量
边上的高,求向量![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 在
在![]() 边上,且
边上,且![]() ,求
,求![]() 的坐标;
的坐标;
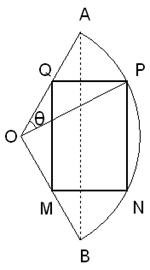
21、(本大题满分12分).我市某校在申办省级示范校期间,征得一块形状为扇形的土地用于建设田径场,如下图所示,已知扇形角![]() ,半径
,半径![]() 米,按要求准备在该地截出内接矩形
米,按要求准备在该地截出内接矩形![]() ,并保证矩形的一边平行于扇形弦
,并保证矩形的一边平行于扇形弦![]() ,设
,设![]() ,记
,记![]() .
.
(Ⅰ)以![]() 为自变量,写出
为自变量,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
 (Ⅱ)当
(Ⅱ)当![]() 为何值时,矩形田径场的面积最大,并求最大面积;
为何值时,矩形田径场的面积最大,并求最大面积;
22、. (本大题满分14分)知向量![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
参考答案
一、选择题:
BDAACBBCCCBD
二、填空题:
13.![]() 14.2 15.(—∞,
14.2 15.(—∞,![]() )
)![]()
16.①③
三、解答题:
17、![]()
18、解:![]() =
=![]()
∵![]() ∴
∴![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]()
当![]() <0时,
<0时,![]() ∴
∴![]()
故![]() 的值为
的值为![]() 或
或![]() 。
。
19、解:由题意知x=![]() y=
y=![]()
∵x⊥y ∴x![]() y=
y=![]()
整理得![]() ,即
,即![]() 注:此题解法不唯一。
注:此题解法不唯一。
20、![]()
![]() 。
。
21、![]()
![]() =
=![]()
当![]()
22 (Ⅰ) ![]() . …………2分
. …………2分
![]() ,
, ![]() …………4分,
…………4分,
即 ![]() .
. ![]() . …………6分
. …………6分
(Ⅱ)![]() …………8分
…………8分
![]() ,
,![]()
![]() ,
,![]() …………10分
…………10分
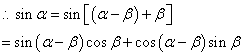 …………12分
…………12分
![]() …………14分
…………14分