三角函数练习题
一、选择题
1、有以下四组角:(1)kπ+ ;(2)kπ- ;(3)2kπ±;(4)-kπ+ (k∈z)其中终边相同的是( )
A、(1)和(2) B、(1)、(2)和(3) C、(1)、(2)和(4) D、(1)、(2)、(3)和(4)
2、若角α的终边过点(sin30°-cos30°),则sinα等于( )
A、 B、- C、- D、-
3、设α= ,则sin(x- )+tg(α- )的值为( )
A、 B、 C、 D、
4、在以下四个函数y=sinx,y=sinx,y=sinx+,y=sin(-x)中,周期函数的个数是( )
A、1 B、2 C、3 D、4
5、若将某正弦函数的图象向右平移 后得到的图象的函数式是y=sin(x+ ),则原来的函数表达式是( )
A、y=sin(x- ) B、y=sin(x+ ) C、y=sin(x+ )- D、y=sin(x+)
6、函数y=sin( -2x)的单调递增区间是( )
A、[kπ- ,kπ+ ] B、[2kπ+ ,2kπ+ ] C、[kπ+ ,kπ+ ] D、[2kπ-,2kπ+] (k∈z)
7、α为第二象限角,其终边上一点为P(x,),且cos=x,则sinα的值为( )
A、 B、 C、 D、-
8、若θ是第三象限的角,且sin >0,则( )
A、cos > B、cos >- C、cos> D、sec <-
9、已知α、β为锐角,且2tgα+3sinβ=7,tgα-6sinβ=1,则sinα的值是( )
A、 B、 C、 D、
10、函数y=sin π的单调增区间是( )
A、[2kπ,(4k+2)π] B、[4k,4k+2] C、[2kπ,(2k+2)π] D、[2k,2k+2] (k∈z)
11、若 =,则x取值范围是( )
A、2kπ≤x≤2kπ+ B、2kπ≤x≤2kπ+π C、2kπ- ≤x≤2kπ+
D、kπ- ≤x≤2kπ+ (k∈z)
12、在[, ]上与函数y=cos(x-π)的图象相同的函数是( )
A、y= B、y= C、y=cos(x-) D、y=cos(-x-4π)
二、填空题:
1、已知tgα=3 则 的值为________
2、函数y= 的定义域是______,值域是______
3、函数y= 的最小正周期是_______
4、函数y=logsin(2x+) 的单调递减区间是______
三、解答题
1、(1)化简: ++cos2αcsc2α
(2)设sin(α+)=-,且sin2α>0
求sinα,tgα
2、已知sinx+≥0, tgx+1≤0求函数y= 的最小值,并求取得最小值y,x的值,此函数有没有最大值,为什么?
3、如果方程x2-4xcosθ+2=0与方程2x2+4xsin2θ-1=0有一根,互为倒数求θ职 (0<θ<π)
4、已知a>0,0≤x<2π,函数y=cos2x-asinx+b的最大值为0最小值为-4,求a和b值,并求出使y取得最大值和最小值时的x值。
解答部分:
一、选择题:
1、D 2、∵γ= =1 ∴sinα= =- ∴选C
3、C 4、C 5、B 6、C 7、A 8、D
| 9、 | { | 2tgα+sinβ=7 tgα-6sinβ=1 |
消β得 tgα=3 ∴ctgα= ∴sin2α= = ∵α为锐角 ∴sinα= ∴选C
10、B 11、B 12、A
二、填空题
1、2
2、由2cos(πx- )-120 得cos(πx- )≥
∴2kπ- ≤πx- ≤2kπ+
∴2k≤x≤2k+ (k∈z)
又 0≤2cos(πx- )-1≤1
∴0≤y≤1
3、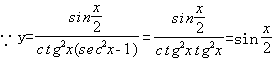
∴T= =4π
4、(kπ- ,kπ+ ) (k∈z)
三、解答题
1(1)原式=+ +cos2αcsc2α
=cos2α+sin2α+cos2αcsc2α
=1+ctg2α
=csc2α
(2)解:由sin(α+ )=-
∴cosα=-
∵sin2α>0
∴2kπ<2α<2kπ+π
kπ<αkπ+ (k∈z)
∴α为第一象限或第二象限的角
∵cosα=- <0
∴α为第三角限角
sinα=-=
tg = =
2、解:由已知sinx≥
∴ x≤2kπ+
tgx≤-1
∴kπ+ <x≤kπ+
∴2kπ+ <x≤2kπ+ (k∈z)
在此范围内y= 是递减函数
∴当x=2kπ+ 时 (k∈z)
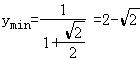
∵它义域为左开右闭区间
∴不存在最大值
3、解:设非零x1为第一方程的根 ∴ <x1为第二方程的根
∴ x12-4x1cos2θ+2=0 ①
2()2+4()sin2θ+2-1=0 ② 由②得:-x12+4x1sin2θ+2=0 ③
①+③得:4x1(cos2θ-sinθ)=4
即 =cos2θ-sin2θ代入②得
2(cos2θ-sin2θ)2+4sin2θ(cos2θ-sin2θ)-1=0
即2(1-2sin2θcos2θ)+4sin2θ-4sin22θ-1=0
∴sin2θ±
∵0<2θ<2π
∴2θ= ,π- ,π+ ,2π-
即θ=,,,
4、解:由y=cos2x-asinx+b
得 y=-sin2x-asinx+1 令t=sinx(-1≤t≤1)
则y=-t2-at+b+1=-(t+)2+ +b+1
①当0<a≤2 时
-(t+ )2最大值为0,最小值为(1+ )2
+b+1=0 -a+b=4 ∴a=2 a=-6 b=-2 b=-10(舍去)