高一上学期期末试卷(数列、不等式检测试卷)
(满分150分,考试时间120分钟)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1、在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8等于
A.45 B.75 C.180 D.300
2、若a>b,c<d,则下列结论中不成立的是
A. a-c>b-c B. a-d>b-c C. a+d>b+c D. a-c>a-d
3、设Sn是等差数列{an}的前n项和,已知S6=36,Sn=324,Sn-6=144(n>6),则n等于
A.15 B.16 C.17 D.18
4、不等式![]() 的解集是
的解集是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5、已知a<0,-1<b<0,则a, ab, ab![]() 之间的大小关系是
之间的大小关系是
A. a>ab> ab![]() B. ab
B. ab![]() >ab>a C.
ab>a> ab D. ab> ab
>ab>a C.
ab>a> ab D. ab> ab![]() >a
>a
6、下列不等式正确的是.
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D) ![]()
7、使x-4+x-5<a有实数解的a的取值范围是
A.a >9 B.1<a <9 C.a >1 D.a ≥ 1
8、设a、b都是正数,则不等式-b<![]() <a的解是
<a的解是
A. -![]() <x<0或0<x<
<x<0或0<x<![]() B. x<
B. x<![]() 或x>
或x>![]()
C. -![]() <x<0或0<x<
<x<0或0<x<![]() D. -
D. -![]() <x<
<x<![]()
9、在数列{an}中,a1=-60,an+1=an+3,则a1+a2+a3+…+a30等于
A.-445 B.765 C.1080 D.3105
10、某人向银行贷款A万元购房,自1年后开始每年向银行等额偿还贷款,10年还清,银行规定年利率为a%并按复利计算,他每年应付给银行的款数为
A.![]() 万元 B.
万元 B.![]() 万元
万元
C. ![]() 万元 D.
万元 D. ![]() 万元
万元
11、Sn为等差数列{an}的前n项之和,若a3=10,a10=-4,则S10-S3等于
A.14 B.6 C.12 D.21
12、各项都是正数的等比数列{an}中,a2,![]() a3,a1成等差数列,则
a3,a1成等差数列,则![]() 的值是
的值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 或
或![]()
二、填空题(本大题共4小题,每小题4分,共16分。)
13、画一个边长为1cm的正方形,再以这个正方形的对角线为边画第二个正方形,以第二个正方形的对角线为边,画第三个正方形,这样一共画了20个正方形,则这20个正方形的周长之和为_______________。
14、已知x>0, 则![]() 的最大值是
。
的最大值是
。
15、已知数列:![]() ,那么它的前n项和为
。
,那么它的前n项和为
。
16、若{bn}的前n项和为Sn=![]() ,则b5+b6=
。
,则b5+b6=
。
三、解答题(本大题共6小题,共74分,解答应写出文字说明或演算步骤)
17、(本小题满分12分)
已知f(x+1)=x2-4.等差数列{an}中,a1=f(x-1),a2=-![]() ,a3=f(x).
,a3=f(x).
(1)求x的值;
(2)求通项公式an
18、(本小题满分12分)
(1) 解不等式![]() .
.
(2)解关于x的不等式![]() .
.
19、(本小题满分12分)
(1) 已知数列{an}是等差数列,d为公差, Sn为前n项和,a1=![]() , d =
, d =![]() ,Sn=-5,求n与an.
,Sn=-5,求n与an.
(2)已知数列{an}是等比数列,q为公比,Sn为前n项和,a1=2,S3=26,求q与a3.
20、(本小题满分12分)
甲、乙两人每次都一起去开远市水泥厂买水泥,甲每次买1000千克水泥,乙每次买1000元钱的水泥,他俩一共买了两次,由于市场价格变化,两次价格都不同,两次买后,谁买的水泥平均价格低?
21、(本小题满分12分)
设数列{an}为等比数列,数列{bn}为等差数列,且b1=0,cn=an+bn,若数列{cn}是1,1,2,…,cn,…. 求数列{cn}的前10项和。
22、(本小题满分14分)
书的每一页都是矩形,在每一页书上所印的文字要占S cm2的矩形,上、下页边处要分别留出a cm的空白,左、右页边处要分别留出b cm的空白,为节约纸张,则每一页面的高和宽分别是多少cm?
数列、不等式检测答卷
(满分150分,考试时间120分钟)
班次 学号 姓名
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 |
二、填空题(本大题共4小题,每小题4分,共16分。)
13、 14、
15、 16、
三、解答题(本大题共6小题,共74分,解答应写出文字说明或演算步骤)
| 17、(本小题满分12分) |
| 18、(本小题满分12分) |
| 19、(本小题满分12分) |
| 20、(本小题满分12分) |
| 21、(本小题满分12分) |
| 22、(本小题满分14分) |
(满分150分,考试时间120分钟)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | C | B | D | C | D | D | C | B | B | D | A | A |
二、填空题(本大题共4小题,每小题4分,共16分。)
13、4092(![]() +1)cm ;14、
+1)cm ;14、![]() ;15、
;15、![]() ;16、
;16、![]() ;
;
三、解答题(本大题共6小题,共74分,解答应写出文字说明或演算步骤)
| 17、(本小题满分12分) 解:①∵f(x+1)=x2-4 ∴a1=f(x-1)=f[(x-2)+1]=(x-2)2-4=x2-4x…………………1分 a3=f(x)=f[(x-1)+1]=(x-1)2-4=x2-2x-3…………………2分 又∵数列{an}是等差数列 ∴2a2=a1+a3…………………4分 即2x(- 2x2-6x=0 ∴x=0或x=3…………………6分 ②当x=0时,a1=0,a2= an=a1+(n-1)d = 当x=3时,a1=-3,a2= an=a1+(n-1)d=-3+(n-1)d = |
| 18、(本小题满分12分) 解:(1)由已知得x>0, …………………1分 ∴2x>0…………………2分 由绝对值不等式的性质得: 因此解得x>1. …………………6分 (2)a=0或a=1时,原不等式无解;…………………8分 0<a<1时,有a2<a,原不等式的解集为{xa2<x<a};…………………10分 a<0 或a>1时,有a2>a,原不等式的解集为{xa<x<a2}.…………………12分 |
| 19、(本小题满分12分) 解:(1) 解得n=15或n=-4(舍去,∵n ∴an=a15=a1+14d= 综上,n=15,an= (2)①当q=1时,∵a1=2,∴S3=6, 这与已知S3=26矛盾,∴q≠1. …………………8分 ②当q≠1时,
解得q=-4或q=3, …………………10分 ∴ |
| 20、(本小题满分12分) 解:设每次购买水泥的价格分别为a元/千克、b元/千克(a≠b),……2分 依题意得 甲购买水泥的平均价格为 乙购买水泥的平均价格为
乙购买水泥的平均价格低。…………………12分 |
| 21、(本小题满分12分) 解:依题意。 c1=a1+b1=1 ∵b1=0 ∴a1=1…………………2分 设bn=b1+(n-1)d=(n-1)d (n∈N*) an=a1·qn-1= qn-1 (n∈N*)…………………3分 ∵ 解得:
∵q≠0∴ ∴an=2n-1 (n∈N*),bn=1-n (n∈N*)…………………9分 ∴ c1+c2+…+c10=(a1+a2+…+a10)+(b1+b2+…+b10) =(1+2+22+…+29)+(0-1-2-…-9) = =210-1-45 =1024-46 =978…………………11分 ∴数列{cn}的前10项和为978. …………………12分 |
| 22、(本小题满分14分) 解:设页面的高为x cm,宽为y cm,…………………2分 则每一页的面积S1=xy cm2. …………………4分 ∵(x-2a)(y-2b)=S, …………………6分 ∴
当且仅当 ………………………………………………………14分。 |
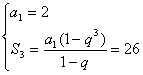 即
即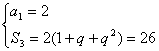
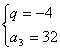 或
或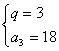 …………………12分
…………………12分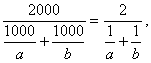 …………………8分
…………………8分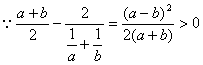 …………………11分
…………………11分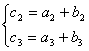 ∴
∴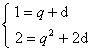 …………………5分
…………………5分