数列综合题

高一（上）数学单元同步练习

第九单元　数列综合题

[重点]

数列的综合应用

1.　　 运用方程的观点解决数列中的应用问题,巧设重要的未知量,用以表达其它的相关量,从而列出所需求解的方程(组)如:

已知四个数,前三个数成等差数列,后三个数成等比数列,可以把这四个数设为

a-d,a,a+d,或。

2．既不是等差数列，又不是等比数列的数列称为杂数列，求这类杂数列前n项和的方法常见的有：（1）化归为等差数列或等比数列的前n项和来求。（2）把每项“裂项”成几项和与差的形工，达到正负相负的目的。（3）由等差数列与等比数列对应项相乘而得的混合数列，可用乘公比“错位相减”后求得结果。（4）对于满足a_n+1=a_n+f(n)形成的数列，可用“累差迭加”的方法求和。

3．等差数列与等比数列的联系性在于：

若{a_n}是等差数列，则{b}(b)是等比数列。

若{a_n}是等比数列，则{log_ba_n}是等差数列。

[难点]

数列的综合应用

一、选择题

1．如果一个数列既是等差数列，又是等比数列，则此数列（　 ）

（A）为常数数列 　　　（B）为非零的常数数列

（C）存在且唯一　　　 （D）不存在

2．已知数列{3}是等比数列，公比为q则数列{a_n}为（　 ）

（A）等比数列，公比为log₃q　　　　　 （B）等差数列，公差为log₃q

（C）等差数列，公差为3^q （D）可能既非等差数列，又非等比数列。

3. 在等差数列{a_n}中，a₁=4,且a₁,a₅,a₁₃成等比数列，则(a_n)的通项公式为（　 ）

（A）a_n=3n+1　　　 　　　　　　　（B）a_n=n+3

（C）a_n=3n+1或a_n=4　　　　　　  （D）a_n=n+3或a_n=4

4．已知a,b,c成等比数列，且x,y分别为a与b、b与c的等差中项，则的值为（　　）

（A）　 （B）-2　 （C）2　　（D） 不确定

5．互不相等的三个正数a,b,c成等差数列，x是a,b的等比中项，y是b,c的等比中项，那么x²,b²,y²三个数（　 ）

（A）成等差数列不成等比数列　　　　　　  （B）成等比数列不成等差数列

（C）既成等差数列又成等比数列　　　　　  （D）既不成等差数列，又不成等比数列

6．在100内能被3整除，但不能被7整除的所有正整数之和为（　 ）

（A）1368　　（B）1470　　（C）1473　 （D）1557

7．数列1，0，2，0，3,…的通项公式为（　 ）

（A）a_n=　　　　　　　　  （B）a_n=

（C）a_n=　　 　　　　　　 （D）a_n=

8.已知数列{a_n}的前n项和为S_n,S_2n+1=4n²+2n,则此数列的通项公式为（　 ）

（A）a_n=2n-2　  （B）a_n=8n-2　　（C）a_n=2^n-1 （D）a_n=n²-n

9.已知(z-x)²=4(x-y)(y-z)，则（　 ）

（A）x,y,z成等差数列　　　　　　  （B）x,y,z成等比数列

（C）成等差数列　　　　　  （D）成等比数列

10．数列{a_n}的前n项和S_n=aⁿ-1，则关于数列{a_n}的下列说法中，正确的个数有（　 ）

①一定是等比数列，但不可能是等差数列 ②一定是等差数列，但不可能是等比数列 ③可能是等比数列，也可能是等差数列 ④可能既不是等差数列，又不是等比数列 ⑤可能既是等差数列，又是等比数列

（A）4　 （B）3　 （C）2　 （D）1

11．由2开始的偶数数列，按下列方法分组：（2），（4，6），（8，10，12），…，第n组有n个数，则第n组的首项为（　 ）

（A）n²-n　  （B）n²-n+2　　（C）n²+n　 （D）n²+n+2

12.数列1,前n项和为（　 ）

（A）n²-　　　　　　　　 （B）n²-

（C）n²-n-　　　　　　　 （D）n²-n-

13.某种细胞开始时有2个，1小时后分裂成4个，并死去1个，2小时后分裂成6个并死去1个，3小时后分裂成10个并死去1个，…，按这种规律进行下去，6小时后细胞的存活数为（　）

（A）67　　（B）71　　（C）65　（D）30

14．已知数列{a_n}的通项公式a_n=5n-1，数列{b_n}满足=,b_n-1=32b_n，若a_n+logb_n 为常数，则满足条件的（　 ）

（A）唯一存在，且值为　　　　　  （B）唯一存在，且值为2

（C）至少存在1个　　　　　　　　  （D）不一定存在

15．若两个等差数列{a_n}、{b_n}的前n项和分别为A_n 、B_n，且满足，则的值为（　 ）

（A）　　　　（B）　　　　（C）　　　 （D）

16．已知数列{a_n}的通项公式为a_n=且S_n=,则n的值为（　　）

（A）98　 （B）99　 （C）100　 （D）101

17．已知数列{a_n}的前n项和为S_n=n²-5n+2,则数列{}的前10项和为（　 ）

（A）56　 （B）58　 （C）62　 （D）60

18．已知数列{a_n}的通项公式为a_n=n+5, 从{a_n}中依次取出第3，9，27，…3ⁿ, …项，按原来的顺序排成一个新的数列，则此数列的前n项和为（　 ）

（A）　　 （B）3ⁿ+5　　（C）　　（D）

19.某人于1995年5月1日去银行存款a元，存的是一年定期储蓄，1996年5月1日他将到期存款的本息一起取出，再加入a元后，还存一年定期储蓄，此后每年5月1日他都按照同样的方法，在银行取款和存款，设银行一年定期储蓄的年利率r不变，则到2000年5月1日，他将所有的存款和利息全部取出时，取出的钱数共有（　 ）

（A）a(1+r)⁴元　　　　　　　  （B）a(1+r)⁵元

（C）a(1+r)⁶元　　　　　　　  （D）元

20.下列命题中是真命题的是(　　)

(A)数列{a_n}是等差数列的充要条件是a_n=pn+q(p)

(B)已知一个数列{a_n}的前n项和为S_n=an²+bn+a,如果此数列是等差数列,那么此数列也是等比数列

(C)数列{a_n}是等比数列的充要条件a_n=ab^n-1

(D)如果一个数列{a_n}的前n项和S_n=abⁿ+c(a0,b0,b1),则此数列是等比数列的充要条件是a+c=0

二、填空题

1．　各项都是正数的等比数列{a_n}，公比q1,a₅,a₇,a₈成等差数列，则公比q=　　　

2．　已知等差数列{a_n}，公差d0,a₁,a₅,a₁₇成等比数列，则=　　　

3．　已知数列{a_n}满足S_n=1+,则a_n=　　　

4．已知二次函数f(x)=n(n+1)x²-(2n+1)x+1,当n=1,2,…，12时，这些函数的图像在x轴上截得的线段长度之和为　　　

5.已知数列{a_n}的通项公式为a_n=log_(n+1)(n+2),则它的前n项之积为　　　

6.数列{(-1)^n-1n²}的前n项之和为　　　

7．一种堆垛方式，最高一层2个物品，第二层6个物品，第三层12个物品，第四层20个物品，第五层30个物品，…，当堆到第n层时的物品的个数为　　　

8．已知数列1，1，2，…，它的各项由一个等比数列与一个首项为0的等差数列的对应项相加而得到，则该数列前10项之和为　　　

9．在2和30之间插入两个正数，使前三个数成等比数列，后三个数成等差数列，则插入的这两个数的等比中项为　　　

10．已知整数对的序列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），……，则第60个数对为　　　　

二、解答题

1.已知数列{a_n}的通项公式为a_n=3ⁿ+2ⁿ+(2n-1),求前n项和。

2．已知数列{a_n}是公差d不为零的等差数列，数列{a_bn}是公比为q的等比数列， b₁=1,b₂=10,b₃=46,，求公比q及bn。

3．已知等差数列{a_n}的公差与等比数列{b_n}的公比相等，且都等于d(d>0,d1),a₁=b₁ ，a₃=3b₃,a₅=5b₅,求a_n,b_n。

4．　有四个数，其中前三个数成等比数列，其积为216，后三个数成等差数列，其和为36，求这四个数。

5．　已知数列{a_n}，前n项和S_n=2n-n²,a_n=log₅bn ，其中bn>0，求数列{bn}的前n项和。

6．　某单位从市场上购进一辆新型轿车，购价为36万元，该单位使用轿车时，一年需养路费、保险费、汽油费、年检费等约需6万元，同时该车的年折旧率为10%（即这辆车每年减少它的价值的10%），试问：使用多少年后，该单位花费在该车上的费用就达36万元，并说明理由。

7．求和S_n=1

8.已知等比数列{a_n}，首项为81，数列{b_n}满足b_n=log₃a_n，其前n项和S_n。

（1）证明{b_n}为等差数列

（2）若S₁₁S₁₂，且S₁₁最大，求{b_n}的公差d的范围

第九单元　  数列综合题

一、选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	B	B	D	C	A	C	B	A	A	C
题号	11	12	13	14	15	16	17	18	19	20
答案	B	A	C	B	D	C	D	D	D	D

8．S_2n+1=(2n+1)²-(2n+1),知S_n=n²-n,a₁=0,当n2时，a_n=S_n-1=2_n-2

10.a_n=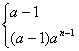　　

当a=0时，数列为-1，0，0，……

当a=1时，数列为0，0，0　……

当a0.a1时，a_n=(a-1)a^n-1,为等比数列。

11．a_n=2n,首项为a_{1+2+…+(n-1)+1}=+1=2[]=n²-n+2

14.bn=2^-5n+4,a_n+logb_n=5n-1+log2^-5n+4=5n-1+(-5n+4)log2,

当-2时，a_n+logb_n=3

15.

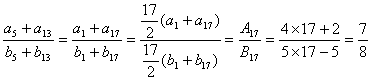
a_n=

18.b_n=a₃ⁿ=3ⁿ+5

19.设95年存入银行为a₁,96年存入银行为a₂,…,则2000年存入银行为a₆，那么2000年从银行取出有 a₆-a元。

a₁=a,a₂=(1+r)a+a,a₃=(1+r)²+(1+r)a+a,

类推得a₆=(1+r)⁵a+(1+r)⁴a+(1+r)³a+(1+r)²a+(1+r)a+a

∴a₆-a=a[(1+r)+(1+r)²+…+(a+r)⁵]=[(1+r)⁶-(1+r)]元

20．（A）a_n=pn+q(qR)　 (B)a=0,若b=0,不为等比数列　　(C) a0、b0

二、　　　　　　 填空题

1. 　　 2. 　　3. 　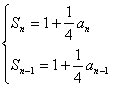　　,相减得a_n=故a_n=-

4. 　　 

5. log₂(n+2)　 6. (-1)^n-1 　 7. n²+n　　8. 978　　 9. 6

10.(5,7)

规律：（1）两个数之和为n的整数对共有n-1个。（2）在两个数之和为n的n-1个整数对中，排列顺序为，第1个数由1起越来越大，第2个数由n-1起来越来越小。设两个数之和为2的数对方第1组，数对个数为1；两个数之和为3的数对为第二组，数对个数2;…… ,两个数之和为n+1的数对为第n组，数对个数为 n。

∵ 1+2+…+10=55，1+2+…+11=66

∴ 第60个数对在第11组之中的第5个数，从而两数之和为12，应为（5，7）

三、解答题

1． S_n=a₁+a₂+…+a_n=(3¹+2¹+1)+(3²+2²+3)+ …+[3ⁿ+2ⁿ+(2n-1)]=(3¹+3²+…+3ⁿ)+(2¹+2²+…2ⁿ)++[1+3+…+(2n-1)]=

2.a=a₁,a=a₁₀=a₁+9d,a=a₄₆=a₁+45d

由{a_bn}为等比数例，得（a₁+9d）²=a₁(a₁+45d)得a₁=3d,即a_b1=3d,a_b2=12d,a_b3=48d.

∴q=4　 又由{a_bn}是{a_n}中的第b_na项，及a_bn=a_b1·4^n-1=3d·4^n-1,a₁+(bn-1)d=3d·4^n-1

∴b_n=3·4^n-1-2

3.∴ a₃=3b₃ , a₁+2d=3a₁d²,  a1(1-3d²)=-2d  ①　 a₅=5b₅, a₁+4d=5a₁d₄ , ∴a₁(1-5d⁴)=-4d　　②　 ②/①,得=2，∴ d²=1或d²=,由题意，d=,a₁=-。∴a_n=a₁+(n-1)d=(n-6)　 b_n=a₁d^n-1=-·()^n-1

4.设这四个数为

则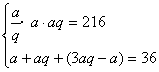　　 由①，得a³=216,a=6　 ③

③代入②，得3aq=36,q=2　 ∴这四个数为3，6，12，18

5.当n=1时，a₁=S₁=1

当n2时，a₁=S_n-S_n-1=3-2n　　 ∴a_n=3-2n　 b_n=5³-2n

∵　 b₁=5　　∴{b_n}是以5为首项，为公比的等比数列。

∴

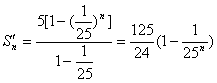
6.用a_n表示该单位第n年花费在轿车上的费用，则

a₁=6+36×0.1　 a₂=6+(36×0.9) ×0.1　 a₃=(36×0.9²) ×0.1

类推可得

a_n=6+(36×0.9^n-1) ×0.1

S_n=a₁+a₂+…+a_n=6_n+36×0.1×[1+0.9+0.9²+…+0.9^n-1]=6n+3.6××+36(1-0.9ⁿ)。

令S_n=36,得n=6×0.9ⁿ　 0.9ⁿ=。

注意到1n6,取值验证，当n=4时，0.9⁴0.6561,,故n4

即使用4年后，花费在轿车上的费用就已达到36万元。

1．　S_n=1·()+3()²+5()³+…+(2n-3)()^n-1+(2n-1)()ⁿ

S_n=1·()²+3()³+…+(2n-3)()ⁿ+(2n-1)()ⁿ⁺¹

两式相减，得

（1-）S_n=1·()+2()²+…+2()ⁿ-(2n-1)

()ⁿ⁺¹=2[()¹+()²+…+(…)ⁿ]-

-(2n-1)( )ⁿ⁺¹=--(2n-1).

即S_n=--(2n-1) ·　

　 S_n=1-

8.(1)设{a_n}的公式为q.

b_n+1-b_n=log₃aⁿ⁺¹-log3a_n=log3=log₃q为常数,做{bn}为等差数列。

（2）b₁=log₃a₁=4

　 　 　 -。
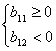
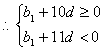