同角三角函数的基本关系式

高一下同步练习卷

4．4 同角三角函数的基本关系式

基础练习

　　1．使成立的x的取值范围是（　）．

　　A．R　　　　 　　　　　　　　　B．，k∈Z，x∈R

　　C．x≠kp，k∈Z，x∈R　　　　　 D．x≠2kp＋p，k∈Z，x∈R

　　2．下列四个命题中正确的是（　）．

　　A．　　　　  B．sina＝0.85，cosa＝0.65

　　C．sina ＝0，cosa ＝－1　　　　  D．tana ＝1，cosa＝－1

　　3．下列等式恒成立的是（　）．

　　A．　　　　  B．tan（2p＋a）·cot（a －2p）＝1

　　C．　　　　  D．

　　4．已知，且270°＜q ＜360°，那么tanq 的值为（　）．

　　A．　　　　　B．　　　　  C．　　　　 D．

　　5．已知，且a 为第一象限角，求sina 、tana 、cota 的值．

　　6．已知，求cosa 、tana 的值．

　　7．已知，求sina 、cosa 、cota 的值．

　　8．在△ABC中，若，则sinA＝________；tanA＝________．

　　9．若a 是第三象限角，且，则sina ＝________；cosa ＝________；tana＝________；

　　10．化简下列各式：

　　（1）sina ·cosa·（tana ＋cota）；

　　（2）；

　　（3）．

　　11．已知，求的值．

　　12．求证：

　　（1）；

　　（2）；

　　（3）．

综合练习

　　1．已知，且tana ＜0，求cosa 及tana 的值．

　　2．已知，且a 是第四象限角，那么cota 的值等于（　）．

　　A． 　　　　 B．　　　　　C．　　　　 D．

　　3．已知，求tana 的值．

　　4．化简的结果是（　）．

　　A．sin6　　　　 B．－sin6　　　 C．sin（6－2p）　D．sin6°

　　5．若sinq cosq ＜0，，则点P（tanq ，sinq －cosq ）位于（　）．

　　A．第一象限　　B．第二象限　　C．第三象限　　D．第四象限

　　6．如果a 是第一象限角，且，那么sina ＝________；cosa ＝________；cota ＝_______．

　　7．已知，求的值．

　　8．若2sina ＝3cosa ，则＝________．

　　9．已知，求sinA·cosA的值．

　　10．已知，且，那么a 是（　）．

　　A．第一、二象限角　　　　　　  B．第二、三象限角

　　C．第三、四象限角　　　　　　  D．第一、四象限角

　　11．如果，那么的值为________．

　　12．化简下列各式：

　　（1）；

　　（2）（a为第三象限角）．

　　13．求证：

　　（1）；

　　（2）；

　　（3）；

　　（4）．

　　14．若，求的值．

　　15．若，求证：x＝y＝0．

　　16．已知，且a 、b 为锐角，求证．

拓展练习

　　1．已知，则（　）．

　　A．　　 　　　　　　B．

　　C．　　　　　 　　　　D．

　　2．，则f（x）的图象是（　）．

　　3．若，且，则的值为________．

　　4．求使等式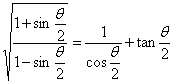成立的角q 的取值范围．

　　5．已知，求的值．

　　6．若关于x的方程的一个根为sina，求证它的另一个根是cosa 或－cosa．

　　7．已知，求证：．

　　8．已知：、tanx、成等差数列，求证tan x、cot x、成等比数列．

参考答案

基础练习

　　1．B． 　 2．C　　3．B 　 4．C

　　5．由，a为第一象限角可得，，．

　　6．∵　，∴　a 为第三象限或第四象限角．当a  为第三象限角时，，；当a 为第四象限角时，，．

　　7．∵　，∴　a 为第二或第四象限角，当a 为第二象限角时，，，cota＝－2；当a 为第四象限角时，，，cota＝－2．

　　8．．．由于cosA＞0，0＜A＜p，故A定为锐角．

　　9．，，．

　　10．（1）原式．

　　（2）原式．

　　（3）原式．

　　11．由已知解得tana＝2．则，得，则．所求式．

　　12．（1）证明：左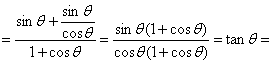式右式．

　　（2）证明：左式

＝＝右式．

　　（3）证明：左式： 右式．

综合练习

　　1．∵　　∴　a为第一或第二象限角，又tana＜0，∴　a 为第二象限角，于是，．

　　2．D．由条件，．

　　3．由m＞1，cosa＞0，a 是第一或第四象限角．当a为第一象限角时，，于是；当a是第四象限角时，，．

　　4．B．原式可得｜sin6｜，又6是第四象限角，故应为－sin6．

　　5．C．由已知可得cosq ＞0，sinq ＜0，故q 是第四象限角．于是tanq ＜0，sinq －cosq ＜0．

　　6．由条件得tana＝1，则，，cota＝1．

　　7．原式化为，将代入原式得，原式．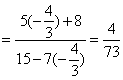

　　8．由已知可得，所求式可化为．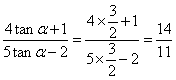

　　9．由，可求得，又＝＝＝＝．

　　10．B．由已知得（t≠0）．

　　11．．由得∴，又.

　　12．（1）原式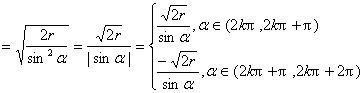k∈Z

　　（2）原式，由于a为第三象限角，故原式．

　　13．（1）左式右式．

　　（2）左式右式．

　　（3）左式＝＝＝右式．

　　（4）左式右式．

　　14．由解得tana＝3．∴　．

　　15．由  得　∴　x＝y＝0得证．

　　16．由a、b为锐角可知a＞0、b＞0，将两式相除可得．即．

　　又由已知条件有，故 ．整理得，.由于a为锐角，，故．

拓展练习

　　1．D．，又

　　2．B．令u＝1+cosx，则cosx＝u－1．，0≤u≤2，即，x∈[0，2]．

　　3．.由可得，又，∴，

　　所求式．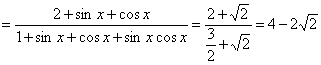

　　4．－p＋4kp＜q＜p＋4kp（k∈Z）．由已知可得．

　　5．由可得，故．

　　原式＝

　　＝．

　　6．设另一个根为u，则由韦达定理可得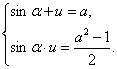∴，即．∴　∴u=±cosa．故该方程的另一个根是cosa或－cosa．

　　7．由得，于是有＝，再变形可得证．

　　8．∵　、tanx、成等差数列，∴　，∴　，cotx＝2，又，解得．于是；，∴　．即tanx、cotx、成等比数列．