| 正弦、余弦的诱导公式 |
1.若![]() ,则
,则![]() ;
;
2.若![]() (
(![]() ),则
),则![]() 。
。
3.化简![]() ,(其中,
,(其中,![]() )得 。
)得 。
4.求值:![]() 。
。
5.化简![]() 。
。
6.设A、B、C是三角形的三个内角,则在:
①![]() ②
②![]()
③![]() ④
④![]() ,
,
这四个式子中,值为常数的有 个。
7.化简:![]() 。
。
8.已知: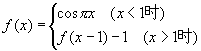
则![]() 的值是 。
的值是 。
9.设![]() ,则
,则![]() 。
。
10.化简:![]() = 。
= 。
【参考答案】
1.![]() ;
;
2.![]()
3.解:![]() 为偶数时,设
为偶数时,设![]()
原式![]()
![]()
![]()
![]() 为奇数时,设
为奇数时,设![]()
原式![]()
![]()
综述原式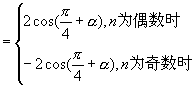
点拨:此类问题应对![]() 的奇偶性进行讨论。再根据诱导公式进行化简。
的奇偶性进行讨论。再根据诱导公式进行化简。
4.答案:原式![]()
![]()
点拨:此类问题先将任意角的三角函数化为锐角函数,再求值。
5.解;原式![]()
![]()
![]()
点拨: 对此类化简问题,先将负角的三角函数化为正角的三角函数,再化为锐角三角函数的值。
6.答案:由![]() ∴
∴ ![]()
∴ ![]() 为常数
为常数
![]() 为常数
为常数
![]() 为常数
为常数
![]() 不为常数
不为常数
∴ 值为常数的式子有3个。
7.答案:原式![]()
8.答案:![]()
![]()
9.答案:![]() 令
令![]()
∴ ![]() ∴
∴![]()
∴![]()
10.0
| 二倍角的正弦、余弦、正切 |
一、填空题
1.已知![]() ,则
,则![]() 。
。
2.若![]() ,化简
,化简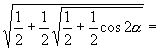 。
。
3.在△ABC中,已知![]() ,则
,则![]() 。
。
4.已知![]() ,则
,则![]() 。
。
5.已知![]() ,则
,则![]() 。
。
二、解答题
6.化简: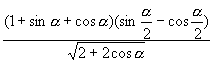 。(其中
。(其中![]() )
)
7.已知![]() ,且
,且![]() ,求
,求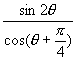 的值。
的值。
8.如果方程![]() 的两根
的两根![]() 与
与![]() 之比为
之比为![]() ,求
,求![]() ,
,![]() 的值。
的值。
9.求函数![]() 的最大值和最小值。
的最大值和最小值。
10.已知:![]() ,
,![]() 与
与![]() 是方程
是方程![]()
![]() 的两根,求
的两根,求![]() 的值。
的值。
【参考答案】
一、填空题
1.![]()
2.![]() (提示:由
(提示:由![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴ 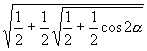
![]()
![]()
![]()
3.![]()
4.![]() (提示:由已知解出
(提示:由已知解出![]() ,∴
,∴![]() )
)
5.-1(提示:由已知解出![]() ,∴
,∴
![]()
二、解答题
6.![]()
7.∵ ![]()
![]()
![]()
∴![]()
![]()
![]()
![]()
故原式![]()
8.∵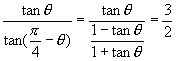 ,
,
∴ ![]() 或
或![]()
当![]() 时
时
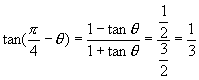
则 ![]()
∴ ![]()
![]()
∴ ![]()
当![]() 时
时
![]()
则 ![]() ∴
∴ ![]()
![]()
9. ![]()
![]() ,
,![]() 。
。
10.![]()
![]()
则 ![]() ,
,![]()
于是从![]() ,知
,知
![]() ,
,![]()
故 ![]()
![]() 。
。