| 正弦函数、余弦函数的图形和性质 |
一、填空题
1．函数
的周期是 ，当
时，
有最小值 。
2．函数
的定义域是 。
3．函数
的最小正周期是 。
4．若函数
（
、
为常数）的最大值为1、最小值为－7，则
的最大值为 。
5．函数
的单调递增区间是 。
二、解答题
1．判断下列函数的奇偶性。
（1）
；
（2）
；
（3）
；
（4）
。
2．求下列函数的定义域。
（1）
； （2）
；
（3）
； （4）
。
3．已知函数
（1）求函数
的最小正周期；
（2）求的最大值、最小值；
（3）求的单调递增区间。
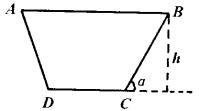
4．水渠横断面为等腰梯形（如图），渠深为
，梯形面积为S，为了使渠道的渗水量达到最小，应使梯形两腰及下底边长之和为最小，问此时腰与下底夹角
应是多少？
5．已知
，则当函数取最大值时，求自变量
的集合。
【参考答案】
一、填空题
1．
、
（
）、
； 2．
（）； 3．
；
4．15； 5．
（）．
二、解答题
1．（1）偶函数；（2）非奇非偶函数；（3）奇函数；（4）既是奇函数又是偶函数。
2．（1）
（）；（2）
（）
（3）
； （4）
3．解：
（1）
（2）
即
，时，最大值2。
即
，时，最小值－2。
（3）
∴
，时，单调递增。
4．解：设
，梯形腰与底边的夹角为，
则
，由梯形面积为定值S。
∴
∴ 
又∵ 
，设梯形两腰及下底和为
，
则
只需求
（
）的最小值。令
∴ 
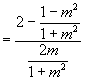
此时
∴
∴ 
∴ 
5．解：
取是大值时，
，
∴ 
，
∴ 函数取最大值时，自变量
的集合为