高一数学第二学期期中试卷
科目 数 学 年级 高二(文科) 命题人 张占友
第I卷
一、选择题（每小题5分，共60分）
1.设集合A和B都是自然数集合N，映射
把集合A中的元素n映射到集合B中的元素
，则在映射f下，象20的原象是 （ ）
A.2 B.3 C.4 D.5
2.函数
（ ）
A.是偶函数，在区间
上单调递增 B. 是偶函数，在区间上单调递减
C.是奇函数，在区间
上单调递增 D. 是奇函数，在区间上单调递减
3.若
，
，则函数
的图像不经过 （ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.若定义在区间
内的函数
满足
，则a的取值范围是（ ）
A.
B.
C. 
D.
5.设
、
都是单调函数，有如下四个命题：
①若单调递增，单调递增，则－单调递增；
②若单调递增，单调递减，则－单调递增；
③若单调递减，单调递增，则－单调递减；
④若单调递减，单调递减，则－单调递减.
其中正确的命题是 （ ）
A. ①③ B. ①④ C. ②③ D. ②④
6.函数
的反函数是 （ ）
A.
B. 
C. 
D. 
7.函数
是单调函数的充要条件是 （ ）
A.
B. 
C. 
D. 
8.甲、乙、丙、丁四人参加奥运会射击项目选拔赛，四人的平均成绩和方差如下表所示：
|
| 甲 | 乙 | 丙 | 丁 |
| 平均数 | 8.5 | 8.8 | 8.8 | 8 |
| 方差 | 3.5 | 3.5 | 2.1 | 8.7 |
则参加奥运会的最佳人选应为 （ ）
A.甲 B.乙 C.丙 D.丁
9.已知
有极大值和极小值，则a的取值范围为 （ ）
A. 
B. 
C. 
或
D. 
或
10.已知函数
，则
的值是 （ ）
A.－2 B.－3 C.1 D.3
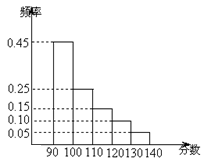
11.某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布图如图所示，若130～140分数段的人数为90人，则90～100分数段的人数为 （ ）
A.900 B.810 C.420 D.270
12.已知是偶函数，且在上单调递增，则
，
，
的大小关系是 （ ）
A.
B.
C.
D.
高一数学第二学期期中试卷(答题纸)
科目 数 学 年级 高二(文科) 命题人 张占友
第Ⅱ卷
二、填空题（每小题4分，共16分）
13.一工厂生产了某种产品16800件，它们来自甲、乙、丙3条生产线。为了检查这批产品的质量，决定采用分层抽样的方法进行抽样。已知从甲、乙、丙3条生产线抽取的个体组成一个等差数列，则乙生产线生产了__________件产品.
14.已知函数
，那么
______________.
15.曲线
的切线中，斜率最小的切线方程为_______________.
16.已知
的反函数为
，若
的图像经过点
，
则b＝____________.
三、解答题（共74分）
17.（本小题满分12分）偶函数
的图像过点
，且在
处的切线方程为
.
（1）求
的解析式； （2）求的极大（小）值.
18. （本小题满分12分）已知函数
，
.
（1）当
时，求函数的最小值；
（2）若对任意，恒成立，试求实数a的取值范围.
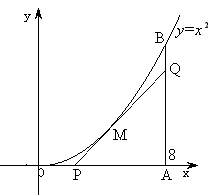19. （本小题满分12分）如图，由
，
，
围成曲边三角形OAB，在曲线OB上求一点M，使得过M所作的曲线的切线PQ与OA，AB围成的三角形PQA的面积最大.
20. （本小题满分12分）已知函数
，其中常数
.
（1）求的定义域、值域；（2）讨论在定义域上的单调性.
21.（本小题满分12分）已知y是x的函数，
，
，其中
.（1）求函数的解析式；
（2）若令的定义域为
，求的值域.
22. （本小题满分14分）已知函数
的图像为曲线E.
（1）若函数
在
和
时取得极值，求a、b的值；
（2）若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a、b满足的关系式；
（3）在（1）的条件下，当
时，
恒成立，求c的取值范围.