高中学生学科素质训练
高一数学同步测试（13）—等比数列
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内.
1．已知
是一个等比数列的前三项，则其第四项等于 （ ）
A．
B．
C．
D．
2．已知
是等比数列且
，
，则
（ ）
A．12
B．10 C．8 D．2＋
3．某厂2001年12月份产值计划为当年1月份产值的n倍，则该厂2001年度产值的月平均增长率为 （ ）
A．
B．
C．
D．
4．在等比数列｛an｝中，若a3 、a9是方程3x2
11x+9=0的两个根，则a6 等于 （ ）
A． 3
B．
3 C．
D．
5．已知数列
的前n项和
，那么下述结论正确的是 （ ）
A．
为任意实数时，是等比数列 B．= －1时，是等比数列
C．=0时，是等比数列 D．不可能是等比数列
6．互不相等的三个正数
成等差数列，
的等比中项，
的等比中项，则
三个数
（ ）
A．成等差数列但不成等比数列 B．成等比数列但不成等差数列
C．既成等差数列又成等比数列 D．既不成等差数列又不成等比数列
7．已知等比数列
中，公比
，且
，那么
等于
（ ）
A．
B．
C．
D．
8．在等比数列中，
，则
等于 （ ）
A．
或
B．
或－
C．
D．
9．某地每年消耗木材约20万
，每价240元，为了减少木材消耗，决定按
征收木材税，这样每年的木材消耗量减少
万，为了既减少木材消耗又保证税金收入每年不少于90万元，则
的范围是 （ ）
A．[1，3] B．[2，4] C．[3，5] D．[4，6]
10．数列中，
是公比为
的等比数列，满足
，则公比
的取值范围是 （ ）
A．
B．
C．
D．
二、填空题：请把答案填在题中横线上.
11．在
之间插入n个正数，使这n+2个正数成等比数列，则插入的n个正数之积
为 ；
12．数列｛
｝中，
且
是正整数)，则数列的通项公式
；
13．若
成等比数列，公比为，则
；
14．已知是等比数列，且，
则
.
三、解答题：解答应写出文字说明、证明过程或演算步骤.
15．三个数成等比数列，若第二个数加4就成等差数列，再把这个等差数列的第三项加32又成等比数列，求这三个数.
16．已知：Sn是等比数列的前n项和，S3，S9，S6成等差数列，求证：
成等差数列.
17．已知函数
构成一个数列，又
.
（1）求数列
的通项公式； （2）比较
与1的大小.
18．在公差不为0的等差数列和等比数列
中，
，
，
，
（1）求数列的公差和数列的公比；
（2）是否存在
使得对于一切自然数
都有
成立？若存在，求出；若不存在请说明理由.
19．某地区位于沙漠边缘地带，到2000年底全县的绿化率只有30%，其余为沙漠化土地，从2001年开始，计划每年把原有沙漠面积的16%栽树改造为绿洲，而同时，原有绿洲面积的4%，又被侵蚀，变成沙漠.
⑴设该地区的面积为1,2000年底绿洲面积为
，经过一年绿洲面积为a2，经过n年绿洲面积为an+1，求an+1与an关系式；
⑵求an的通项公式；
⑶问至少需要经过多少年的努力，才能使该地区的绿洲面积超过60%？（年数取整数，
lg2≈0.3010）
20．已知
且
，数列是首项为
，公比为的等比数列，令
，
（1）当
时，求数列的前项和
；
（2）若数列中的每一项总小于它后面的项时，求的取值范围.
高一数学（上）同步测试（13）参考答案
一、 选择题：ABDCB ABACD
二、 填空题：
11、 
； 12、
； 13、1； 14、5. 13、解：由题意得：
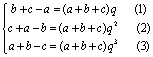
（1）+（2）+（3）得：
∵
，∴=1．
三、 解答题：15、解：按等差数列设原数列三个数为：b—d,b—4,b+d，由已知：三个数成等比数列，即
①
②
由①、②联立.解得：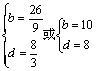
，∴
.
16、证明：∵S3，S9，S6成等差数列
∴S3+S6=2S9
若q=1，则S3=3
由
，与题设矛盾.
整理，得q3+q6=2q9
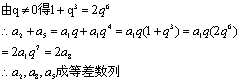
17、解：（1）
（2）
（错位相减）.
18、解：（1）设的公差为
，的公比为，由已知：，
，
，
解得
（舍去）或
，（2）若存在，使得成立，即
，∴
，
∴
要使上式对于一切自然数成立，必须且只需
，解得
，因此，存在
使得结论成立.
19、解：（1）设2000年底沙漠面积为b1，经过n年后沙漠面积为bn+1，则
.
an+1=96%·an+16%bn=96%an+16%（1－an）=
（2）由
是以
为首项，
为公比的等比数列
依题意，
；
（3）
，故至少需要经过5年才能使全地区的绿洲面积超过60%.
20、解：（1）由题意得：
，则
，
当时
，∴
…
①
…
②
①②得：
…
， ∴
；
（2）由题意得：
， ∴
，
当
时，
则
∴，当
时，
即
则
∴
，综上所述，满足条件的范围为：或
.