高一数学期末综合检测

高一数学期末综合检测

 (满分150分，时间120分钟)

一、选择题(5′×12＝60分)

1.若全集S＝R，M＝｛x｜x²-2x-3<0｝，P＝｛x｜lg(x+1)<1｝，则为(　　)

A.(-∞，-1)∪［3，9］　　　　　  　　　 B.(-1,3)

C.(-1,9)　　　　　　　　　　　　　　　　　　D.［3，9)

2.如果函数f(x)＝x²+2(m-1)x+2在区间(-∞，4)上是减函数，那么实数m的取值集合是(　　)

A.｛m｜m≤-3｝　　　B.｛m｜m≥3｝　　　 C.｛m｜m≥-3｝　　　D.｛m｜m≤5｝

3.已知P＝｛x｜｜x｜≤3｝，Q＝｛x｜x>a｝，P∩Q＝φ，则实数a的取值范围是(　　)

A.(-∞，-3)　　　　 B.(-∞，3)　　　　　C.［3，+∞］　　　　　　D.(3，+∞)

4.若函数f(x)的图像经过点(0，1)，则函数f(x+2)的反函数的图像必经过点(　　)

A.(1，-2)　　　　　 B.(2，-1)　　　　　 C.(-2，1)　　　　　 D.(1，2)

5.使对数式log_2x(5x-1)>0成立的一个必要而非充分条件是(　　)

A.｛x｜x>｝　　　　　　　　　　　　　 B.｛x｜<x<,或x>｝

C.｛x｜<x<1｝　　　　　　　　　　　　 D.｛x｜0<x<,或x>｝

6.若等比数列｛a_n｝的前n项和S_n＝3ⁿ+m，则m的值为(　　)

A.3　　 　　　　　　B.0　　　　　　　　 C.-1　　　　　　　　D.任意实数

7.若两个等差数列｛a_n｝,｛b_n｝前n项和A_n,B_n满足A_n∶B_n＝(7n+1)∶(4n+27)，则a₁₁∶b₁₁＝(　　)

A.7∶4　　　　　　　B.3∶2　　　　　　　C.4∶3　　　　　　　D.78∶71

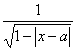8.已知函数f(x)＝的定义域为M，g(x)＝的定义域为P，若M∩P＝，则实数a的取值范围是(　　)

A.(-2，4)　　　　　 B.［-1，3］　　　　 C.［-2，4］　　　　 D.(-1，3)

9.若集合M＝≠，则实数m的取值范围是(　　)

A.(7，+∞)　　　　　B.(1，+∞)　　　　　C.［1，+∞］　　　　　　D.(1,7)

10.已知2<a<，函数f(x)是定义在区间(-1，1)上的偶函数，且有f(a-2)-f(4-a²)<0，则f(x)(　　)

A.在(-1，1)上单调递减　　　　　　　　　 B.在(-1，1)上单调递增

C.在(-1，0)上单调减，在(0，1)上单调增　 D.在(-1，0)上单调增，在(0，1)上单调减

11.设｛a_n｝是由正数组成的等比数列，公比q＝2,且a₁a₂a₃…a₃₀＝2³⁰，则a₃a₆a₉…a₃₀＝(　　)

A.2¹⁰　　　　　　　　B.2²⁰　　　　　　　　C.2¹⁶　　　　　　　　D.2¹⁵

12.设2^a＝3,2^b＝6,2^c＝12，则数列a,b,c(　　)

A.是等差数列，但不是等比数列　　　　　　B.是等比数列，但不是等差数列

C.既是等差数列，又是等比数列　　　　　　D.既不是等差数列，又不是等比数列

二、填空题(4×4＝16分)

13.命题“整数a,b都是偶数时，a+b是偶数”的否命题是　　　　　  ，否命题是_________命题(填真或假).

14.在数列｛a_n｝中，a_n＝，其中a、b、c均为正常数，则这个数列的单调性是　　　　　  .

15.已知函数f(x)＝｜3^x-1｜,a>b>c,且f(c)>f(a)>f(b)，那么3^a+3^c与2的大小关系是　　　　  　　.

16.计算S＝1+++…+的结果是　　　　　  (n∈N^*).

三、解答题(10′+10′+12′+14′+14′+14′)

17.已知log_am＝4，log_an＝5.

求M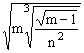＝的值.

18.已知函数y＝的值域是｛y｜y≤0｝∪｛y｜y≥3｝，求此函数的定义域.

19.已知函数f(x)是(-∞，+∞)上的增函数，a,b∈R.

(1)证明：若a+b≥0，则f(a)+f(b)≥f(-a)+f(-b)

(2)判断(1)的逆命题是否成立，并证明你的结论.

20.已知函数f(x)＝.

(1)试判断这个函数的奇偶性、单调性，并求出其值域；

(2)解不等式0<f(x²-x-2)<.

21.某工厂在“减员增效”工作中，规定下岗人员第一年可以到原单位领取全额工资，从第二年起，以后每年只能在原单位按上一年工资额的领取.该工厂根据下岗人员特长，创办新的经济实体.该实体预计第一年属投资阶段，没有利润，因而职员均无收入.第二年每人年收入可达b元，从第三年起每人年收入可在上一年的基础上递增.如果某工人下岗后立即转入这个创办的经济实体，又设该工人下岗前的年工资额为a元.

(1)求这位工人下岗后第n年的年收入a_n的表达式；

(2)当b＝()⁵a时，这位工人哪一年的收入最少?最少年收入是多少?

22.已知数列｛a_n｝满足条件：a₁＝1,a₂＝r(r>0)，且数列｛a_na_n+1｝是公比为q(q>0)的等比数列，设b_n＝a_2n-1+a_2n.

(1)求使不等式a_na_n+1+a_n+1a_n+2>a_n+2a_n+3成立的q的取值范围；

(2)设r＝2^19.2-1,q＝，求数列｛｝的最大项和最小项.

参考答案:

一、1.D　2.A　3.C  4.A　5.B　6.C  7.C　8.B　9.A  10.C　11.B　12.A

二、13.整数a、b不都是偶数时，a+b是奇数，假.　14.单调递增数列.　15.3^a+3^c＜2　　16.

三、17.1　　18.｛x｜≤x≤2，x≠1｝　　19.略　　20.①奇函数，增函数，定义域R，值域为(-1，1).提示：用定义判断奇偶性.单调性.求值域时利用反函数，但要分y=1和y≠1两种情况考虑.

②｛x｜-2＜x＜-1，或2＜x＜3｝.提示：注意f(0)=0.f(4)=，原不等式为f(0)＜f(x²-x-2)＜f(4)，由f(x)为增函数知0＜x²-x-2＜4.

21.①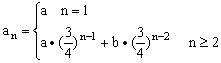

②第4年收入量最少，最少为a元.

22.①0＜q＜.

②最大项C₂₁=2.25，最小项C₂₀=-4.提示：数列｛b_n｝是以q为公比，首项为1+r的等比数列，即b_n=(1+r)q^n-1.

设C_n==…=1+，当n≥21时，｛C_n｝为递减数列；当n≤20时，｛C_n｝亦为递减数列，即C₂₀≤C_n≤C₂₁.