高一数学期末综合练习(一)
【课内四基达标】
一、选择题
1.下列四个命题:①若|a|=0,则a=0,②|a|=|b|,则a=b,或a=-b③若a与b是平行向量,则|a|=|b| ④若a=O,则-a=O.其中正确命题个数是( )
A.3 B.2 C.1 D.0
2.已知函数f(x)=![]() (cotx-1)(cos2x-1),则f(
(cotx-1)(cos2x-1),则f(![]() )等于( )
)等于( )
A.![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
3.设a+b=(2,-8),a-b=(-8,16),则a与b夹角为( )
A.π-arccos![]() B.π+arccos
B.π+arccos![]()
C.-arccos![]() D.arccos
D.arccos![]()
4.设tanx=2,则![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() C.-
C.- ![]() D.
D. ![]()
5.设![]() =(1,3),
=(1,3),![]() =(2,-1),向量
=(2,-1),向量![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,则
,则![]() 是( )
是( )
A.(7,14) B.(14,7) C.(2,-1) D.(-1,2)
6.函数y=2sinx·cos2x+sinx的最小正周期是( )
A.2π B.π C. ![]() π D.
π D. ![]()
7.△ABC的三边长分别为|![]() |=7,|
|=7,|![]() |=5,|
|=5,|![]() |=6,则
|=6,则![]() ·
·![]() 的值为( )
的值为( )
A.38 B.-38 C.19 D.-19
8.已知向量a=(2cosφ,2sinφ),φ∈(![]() ,π),b=(0,1),则a与b的夹角为( )
,π),b=(0,1),则a与b的夹角为( )
A. ![]() -φ B.
-φ B.
![]() +φ C.φ-
+φ C.φ-![]() D.φ
D.φ
9.函数f(x)=lg![]() 是( )
是( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数
10.设i,j是平面直角坐标系内x轴,y轴正方向上的两个单位向量,且![]() =4i-2j,
=4i-2j, ![]() =7i+4j,
=7i+4j, ![]() =3i+6j,由四边形ABCD的面积是( )
=3i+6j,由四边形ABCD的面积是( )
A.20 B.5![]() C.45 D.30
C.45 D.30
二、填空题
11.已知|a|=2,|b|=1,a与b夹角为30°,则|![]() a-b|的值为
.
a-b|的值为
.
12.在平面四边形ABCD中,![]() =a,
=a, ![]() =b,
=b, ![]() =c,
=c, ![]() =d,且a·b=b·c=c·d=d·a,则四边形ABCD是
.
=d,且a·b=b·c=c·d=d·a,则四边形ABCD是
.
13.已知|a|=![]() ,|b|=3,a与b的夹角为30°,则a+λb与λa+b的夹角为锐角时,λ的取值范围是
.
,|b|=3,a与b的夹角为30°,则a+λb与λa+b的夹角为锐角时,λ的取值范围是
.
14.△ABC的各顶点坐标分别为A(-1,2)、 B(3,-1)、 C(-5,3),D是BC上一点,若
S△ABD=![]() S△ABC,则D的坐标是
.
S△ABC,则D的坐标是
.
三、解答题
15.若△ABC的三个内角的A、B、C成等差数列,A为最小角,且![]() cos
cos![]() =sinA+sinC,求∠A的大小.
=sinA+sinC,求∠A的大小.
16.设a=(1+cosα,sinα),b=(1-cosβ,sinβ),c=(1,0),α∈(0,π),β∈(π,2π), a与c的夹角为θ1,b与c的夹角为θ2,且θ1-θ2=![]() ,求sin
,求sin![]() 的值.
的值.
17.已知a=(![]() ,-1),b=(
,-1),b=(![]() ,
,![]() )
)
(1)证明:a⊥b;(2)若存在不同时为零的实数k和t,使x=a+(t2-3)b,y=-ka+tb,且x⊥y.试求函数关系式k=f(t);(3)讨论关于t的方程f(t)-tk=0的解的情况.
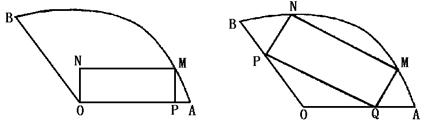
18.将一块圆心角为120°,半径为20cm的扇形铁片裁成一块矩形,如图有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
【能力素质提高】
1.任意给定4个定点A、B、C、D,求![]() ·
·![]() +
+![]() ·
·![]() +
+![]() ·
·![]() 的值.
的值.
2.已知3a-2b=(-2,4),c=(-2,2),a·c=2,|b|=4,求b与c的夹角.
3.已知a=(cosα,sinα),b=(cosβ,sinβ),a与b之间有关系|ka+b|=![]() |a-kb|,其中k>0
|a-kb|,其中k>0
(1)用k表示a,b;
(2)求a、b的最小值,并求此时a、b的夹角的大小.
【综合实践创新】
1.若d=(a·c)·b-(a·b)·c,求a与d的夹角.
2.在正三角形ABC中,|![]() |=a,则
|=a,则![]() ·
·![]() +
+![]() ·
·![]() +
+![]() ·
·![]() 的值为多少?
的值为多少?
3.已知|a|=2,|b|=2,a+b=(3, ![]() ),求向量a与b的夹角.
),求向量a与b的夹角.
【高考真题演练】
1.已知α是第三象限角且sinα=-![]() ,则tan
,则tan![]() =( )
=( )
A. ![]() B.
B. ![]() C.-
C.- ![]() D.-
D.-
![]()
2.![]() 的值为
.
的值为
.
3.一个直角三角形三内角的正弦值成等比数列,其最小内角为( )
A.arccos![]() B.arcsin
B.arcsin![]()
C.arccos![]() D.arcsin
D.arcsin![]()
4.若sinα>tanα>cotα(-![]() <α<
<α<![]()
![]() 则α∈( )
则α∈( )
A.(- ![]() ,-
,-![]() ) B.(-
) B.(- ![]() ,0)
,0)
C.(0,![]() ) D.(
) D.( ![]() ,
,![]() )
)
5.若f(x)sinx是周期为π的奇函数,则f(x)可以是( )
A.sinx B.cosx C.sin2x D.cos2x
6.在△ABC中,角A、B、C对边分别为a、b、c,证明:![]() =
=![]()
参考答案
【课内四基达标】
一、1.C 2.B 3.A 4.D 5.A 6.C 7.D 8.C 9.C 10.D
二、11.![]() 12.矩形 13.λ<
12.矩形 13.λ<![]() 或λ>
或λ>![]() 14.(1,0)
14.(1,0)
三、15.解
A、B、C等差![]() 2B=A+C
2B=A+C![]() B=60° A+C=120°
B=60° A+C=120°
又∵![]() cos
cos![]() =sinA+sinC
=sinA+sinC![]()
![]() cos
cos![]() =2sin
=2sin![]() cos
cos![]()
![]()
![]() cos
cos![]()
![]() cos
cos![]() =cos
=cos![]() 又∵A为最小角 ∴
又∵A为最小角 ∴![]() =
=![]()
![]() C=2A
C=2A
∴A+2A=120°![]() A=40°
A=40°
16.解
∵a=(2cos2![]() ,2sin
,2sin![]() cos
cos![]() )=2cos
)=2cos![]() (cos
(cos![]() ,sin
,sin![]() )
)![]() θ1=
θ1=![]()
b=(2sin2![]() ,2sin
,2sin![]() cos
cos![]() )=2sin
)=2sin![]() (sin
(sin![]() ,cos
,cos![]() )
) ![]() θ2=
θ2=![]() -
- ![]()
∴θ1-θ2=![]() +
+ ![]()
=![]()
![]()
![]() =-
=-![]()
∴sin![]() =sin(-
=sin(-![]() )=-
)=-![]()
17.解:(1)证明:∵a·b=![]() ×
×![]() +(-1)×
+(-1)×![]() =
=![]() -
-![]() =0 ∴a⊥b
=0 ∴a⊥b
(2)∵x⊥y![]() ∴x·y=0
∴x·y=0![]() -ka2+t(t2-3)b2=0
-ka2+t(t2-3)b2=0![]() -4k+t(t2-3)=0
-4k+t(t2-3)=0
![]() k=f(t)=
k=f(t)=![]() t(t2-3)
t(t2-3)
(3)f(t)-tk=0![]()
![]() t(t2-3)-tk=0
t(t2-3)-tk=0![]() t=0或k=
t=0或k=![]() (t2-3)
(t2-3)
当k>0时,原方程有三解.
当k=0时,原方程有两解.
当-![]() <k<0时,原方程有三解.
<k<0时,原方程有三解.
当k=-![]() 时,原方程有一解
时,原方程有一解
当k<-![]() 时,原方程有一解
时,原方程有一解
总之 当-![]() <k<0时或k>0时,原方程有三解
<k<0时或k>0时,原方程有三解
当k=0时,原方程有两解
当k≤-![]() 时,原方程有一解
时,原方程有一解
18.解:第一种截法,连结OM.设∠MOP=θ,则
MP=20sinθ OP=20cosθ S=MP·OP=200sin2θ
当2θ=90°时,即θ=45°时 Smax=200(cm2)
第二种截法:连结OM.设∠MOP=θ,则
MN=40sin(60°-θ) QM=![]() sinθ=
sinθ=![]()
![]() sinθ
sinθ
∴S=MN·QM=![]()
![]() (60°-θ)sinθ=-
(60°-θ)sinθ=-![]()
![]() [cos60°-cos(60°-2θ)]=
[cos60°-cos(60°-2θ)]=![]() [cos(60°-2θ)-
[cos(60°-2θ)- ![]() ]
]
当60°-2θ=0°![]() θ=30°时Smax=
θ=30°时Smax=![]() (cm2)
(cm2)
又∵![]() >200 ∴第二种截法能得到最大面积的矩形。这个最大值为
>200 ∴第二种截法能得到最大面积的矩形。这个最大值为![]() (cm2)
(cm2)
【能力素质提高】
1.解原式=![]() ·
·![]() +
+![]() ·
·![]() +(
+(![]() +
+![]() )=
)=![]() ·
·![]() )·
)·![]() =(
=(![]() +
+![]() )·
)·![]() +
+![]() ·(
·(![]() +
+![]() )=
)=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() ·(
·(![]() +
+![]() )=0
)=0
2.解:(3a-b)c=4![]() 3a·c-2b·c=4
3a·c-2b·c=4![]() 6-2×|b||c|cosθ=4
6-2×|b||c|cosθ=4![]() 6-2×4×2
6-2×4×2![]() cosθ=4
cosθ=4![]() cosθ=
cosθ=![]()
![]() θ=arccos
θ=arccos![]()
3.解:(1)|ka+b|=![]() |a-kb|2
|a-kb|2![]() |ka+b|=3|a-kb|2
|ka+b|=3|a-kb|2![]() k2+2kab+1=3-6kab+3k2
k2+2kab+1=3-6kab+3k2![]() 8kab=2(k2+1)
8kab=2(k2+1) ![]() a·b=
a·b=![]() (k>0)
(k>0)
(2) a·b=![]() (k+
(k+![]() )≥
)≥![]() ∴a·bmin=
∴a·bmin=![]()
此时 cosθ=![]()
![]() θ=60°
θ=60°
【综合实践创新】
1.解:∵a·d=a[(a·c)·b-(a·b)·c]=(a·c)·(a·b)-(a·b)·(a·c)=0
∴a⊥d即a与d的夹角为90°
2.解:原式:a2·cos120°+a2cos120°+a2cos120°=-![]() a2
a2
3.解:∵a+b=(3, ![]() )
) ![]() a2+2ab+b2=12
a2+2ab+b2=12![]() 4+2·2·2cosθ+4=12
4+2·2·2cosθ+4=12![]() cosθ=
cosθ=![]()
![]() θ=60°.
θ=60°.
【高考真题演练】
1.D 2.2-![]() 3.B 4.B
5.B
3.B 4.B
5.B
6.证明:由余弦定理 a2=b2+c2-2bccosA
b2=a2+c2-2accosB
∴a2-b2=b2-a2-2bccosA+2accosB
整理得 ![]() =
=![]()
依正弦定理有:![]() =
=![]()
![]() =
=![]()
∴![]() =
=![]() =
=![]()