高中学生学科素质训练
高一数学期中测试题
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
|
一、选择题（每小题5分，共60分，请将所选答案填在括号内）
1．若
为锐角，且
，则
等于 （ ）
A．
B．
C．
D．
2．设
，若
则
等于 （ ）
A．
B．
C．
D．
3．
等于 （ ）
A．0 B．
C．
D．
4．函数
的单调递减区间是 （ ）
A．
B．
C．
D．
5．函数
的最小正周期为 （ ）
A．
B．
C．
D．
6．函数
的值域为 （ ）
A．
B．[
] C．[
，1] D．[－1，
]
7．函数
的一条对称直线是（ ）
A．
B．
C．
D．
8．已知
是第二象限角，下列四个不等式 （ ）
①
②
③
④
可能成立的是 （ ）
A．①② B．①③ C．②③ D．③④
9．把函数
的图象向右平移
个单位，所得图象正好关于
轴对称，则的最小正值是 （ ）
A．
B．
C．
D．
10．把函数
的图象和直线
围成一个封闭的图形，则这个封闭图形的面积为 （ ）
A．4 B．8 C．2 D．4
11．已知、
均为锐角，
，则、大小关系为 （ ）
A．
B．
C．
D．不能确定
12．已知、为锐角，2
则等于 （ ）
A．
B．
C．
D．
|
二、填空题（每小题4分，共16分，请将答案填在横线上）
13．
， 则
.
14．
.
15．设
则
的定义域为
.
16．已知
，则
.
三、解答题（本大题共74分，17—21题每题12分，22题14分）
|
17．在△ABC中，A、B、C的对边为a、b、c，且a、b、c成等比数列，
求：（1）求角B的范围；
（2）求
的最值.
|
18．已知函数
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）指出的周期、振幅、初相；
（3）说明此函数图象可由
上的图象经怎样的变换得到.
|
19．求函数
的值域.
|
20．已知圆的内接四边形ABCD的边长分别为AB=2，BC=6，
CD=DA=4，求四边形ABCD的面积.
|
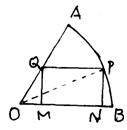
21．将一块圆心角为60°，半径为20cm的扇形铁电裁成一个矩形，
求裁得矩形的最大面积.
|
22．已知、
，且
角和满足条件
（1）用
表示
；
（2）求的最大值.
高一下学期期中测试题数学参考答案
一、1．A 2．C 3．A 4．C 5．C 6．A 7．C 8．D 9．C 10．D 11．B 12．C
二、13．
14．
15．[－3，1] 16．
三、17．（1）
故
（2）
18．（1）略. （2）A=3，T=4，
（3）略.
19．令
且 
有
.
20．连结BD，则有四边形ABCD的面积
∵A+C=180° 
有S=16
由余弦定理：
BD2=AB2+AD2－2AB·AD·
BD2=CB2+CD2－2CB·CD·
解之
又0°＜A＜180° ∴A=120°，
|
，则PN=
SMNPQ=
当
时
SMNPQ取最大值
22．（1）
（2）令
则
即
由
且
, 可知
的最大值为