高一数学上学期高一期中考试题3
(时间90分钟)
一、选择题(共12小题,每小题4分)
1、设全集U={a,b,c,d,e},集合M={ a,c,d},N={b,d,e},那么M∩CUN是( )
A、φ B、{d} C、{a,c} D、{b,e}
2、命题“若![]() ,则
,则![]() ”与其逆命题、否命题、逆否命题这四个命题中,真命题是( )
”与其逆命题、否命题、逆否命题这四个命题中,真命题是( )
A. 原命题、否命题 B. 原命题、逆命题
C. 原命题、逆否命题 D. 逆命题、否命题
3、下列结论错误的是 ( )
A. 原命题为真,其逆命题不一定为真;
B. 原命题为真,其否命题不一定为真;
C. 逆命题为真,否命题就一定为真;
D. 原命题为真,逆否命题不一定为真
4、下列命题中正确的是( )
(A)任何一个集合![]() 必有两个子集;
必有两个子集;
(B)任何一个集合![]() 必有一个真子集;
必有一个真子集;
(C)如果集合![]() 和
和![]() 的交集是空集,则
的交集是空集,则![]() 中至少有一个为空集;
中至少有一个为空集;
(D)如果集合![]() 和
和![]() 的交集是全集,则
的交集是全集,则![]() 都是全集.
都是全集.
5、设集合![]() ,
,![]() ,则( )
,则( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6、已知P={x||x|≤3},Q={x|x>a},P∩Q=φ,则实数a的取值范围是( )
A.(-∞,-3) B.(-∞,3) C.[3,+∞) D.(3,+∞)
7、若集合M=![]() ≠
≠![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.(7,+∞) B.(1,+∞) C.[1,+∞) D.(1,7)
8、集合{1,2,3}的真子集共有( )
(A)5个 (B)6个 (C)7个 (D)8个
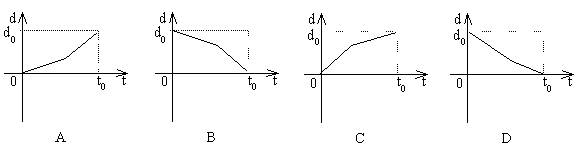
9、某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程。在下列各图中,纵轴表示离家的距离,横轴表示出发后的时间,则下列各图中,较符合该学生走法的是( )
 10、已知
10、已知![]() ,则
,则![]() 等于( )
等于( )
(A)![]() ;(B)
;(B)![]() ;(C)
;(C)![]() ;(D)
;(D)![]()
11、集合A={x![]() }
}![]() {x
{x![]() },集合B=(-
},集合B=(-![]() ,-1)
,-1)![]() (1,2)
(1,2)![]() (2,+
(2,+![]() ),则A、B之间的关系是( )
),则A、B之间的关系是( )
(A)A=B
(B)A![]() B
B
(C)A![]() B
(D)A
B
(D)A![]() B
B
12、f(x)是一次函数且2f(1)+3f(2)=3,2f(-1)-f(0)=-1,则f(x)等于( )
(A)![]() (B)36x-9
(B)36x-9
(C)![]() (D)9-36x
(D)9-36x
二、填空题(共4小题)
13、(4分)若![]() ,那么关于
,那么关于![]() 的不等式
的不等式![]() 的解集为___________。
的解集为___________。
14、(4分)命题“整数a,b都是偶数时,a+b是偶数”的否命题是 ,否命题是_________命题(填真或假).
15、(4分)若A={1,4,x},B={1,x2}且A![]() B=B,则x=
B=B,则x=
16、(4分)若f(![]() (x>0),则f(x)=
(x>0),则f(x)=
![]() 高一数学上学期高一期中考试题3
高一数学上学期高一期中考试题3
一、选答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空:
13、____________;14、_______________、______________;15、_______________;16、__________________。
解答题(共3小题)
17、(12分)已知p: x2-8x-20>0, q: x2-2x+1-a2>0若p是q充分而不必要条件,
求:实数a的取值范围
18、(12分)设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+1=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域。
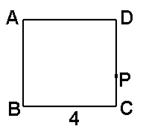 19、(12分)如图,在边长为4的正方形ABCD的边上有动点P,从B点开始,沿折线BCDA向A点运动,设点P移动的路程为x,
19、(12分)如图,在边长为4的正方形ABCD的边上有动点P,从B点开始,沿折线BCDA向A点运动,设点P移动的路程为x,![]() ABP面积为S.
ABP面积为S.
(1) 求函数S=f(x)的解析式、定义域和值域;
(2) 求f[f(3)]的值。
选作题:(10分)设函数![]() ,其中
,其中![]() 。
。
(I)解不等式![]() ;
;
(II)求![]() 的取值范围,使函数
的取值范围,使函数![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。
参考答案
一、选择题(共12小题)
1、C 2、C 3、D4、5、B6、C7、A8、C9、C10、11、C12、C
二、填空题(共4小题)
13、![]() 14、整数a、b不都是偶数时,a+b是奇数,假.
14、整数a、b不都是偶数时,a+b是奇数,假.
15、0,![]() 16、)f(x)=
16、)f(x)=![]()
令![]() 即得f(t)。
即得f(t)。
三、
解答题(共3小题)
17、(12分)0<a≤3.
18、(12分)∵x1,x2是x2-2(m-1)x+m+1=0的两个实根,∴ ![]() =4(m-1)2-4(m+1)
=4(m-1)2-4(m+1)![]() 0,解得m
0,解得m![]() 或m
或m![]() 3。
3。
又∵x1+x2=2(m-1),x1·x2=2(m-1),x1·x2=m+1,
∴y=f(m)=x12+x22=(x1+x2)2-2x1x2=4m2-10m+2,即y=f(m)=4m2-10m+2(m![]() 0或m
0或m![]() 3)
3)
19、(12分)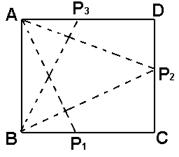 如图所示,
如图所示,
S![]() ABP1=
ABP1=![]() ×4×x=2x,0<x
×4×x=2x,0<x![]() ;
;
S![]() ABP2=
ABP2=![]() ×4×4=8,4<x
×4×4=8,4<x![]() ;
;
S![]() ABP3
ABP3![]() ×4×(12-x)=24-2x,8<x<12。
×4×(12-x)=24-2x,8<x<12。
![]() S=f(x)=
S=f(x)=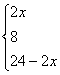
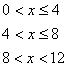
![]() 定义域为(0,12);
定义域为(0,12);
值域为(0,8)![]() {8}
{8}![]() (0,8)=(0,8);f[f(3)]=f(6)=8。
(0,8)=(0,8);f[f(3)]=f(6)=8。
选作题:解:(I)不等式![]() 即
即
![]() ,
,
由此可得![]() ,即
,即![]() ,其中常数
,其中常数![]() 。
。
所以,原不等式等价于
![]()
即 ![]()
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() 。
。
(II)在区间![]() 上任取
上任取![]() ,
,![]() ,使得
,使得![]() <
<![]() 。
。
![]()
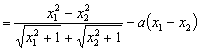
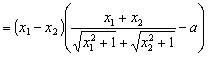 。
。
当![]() 时,
时,
∵ ![]() ,
,
∴ ![]() ,
,
又 ![]() ,
,
∴ ![]() ,
,
即 ![]() 。
。
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调递减函数。
上是单调递减函数。
(ii)当![]() 时,在区间
时,在区间![]() 上存在两点
上存在两点![]() ,
,![]() ,满足
,满足
![]() ,
,![]() ,即
,即![]()
![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上不是单调函数。
上不是单调函数。
综上,当且仅当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。