高一数学上学期期末试卷1
一. 选择题(共10个小题,每题4分)
1. 已知函数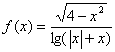 ,则它的定义域为( )
,则它的定义域为( )
A. ![]()
![]() B.
B.
![]()
![]()
C. ![]()
![]() D.
D.
![]()
2. 函数![]() 在
在![]() 上为增函数,则a的取值范围是( )
上为增函数,则a的取值范围是( )
A. ![]() B.
B.
![]()
C. ![]()
![]() D.
D.
![]()
3. 若函数![]() 在
在![]() 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 设![]()
![]() 是公差小于0的等差数列,它的前n项和为
是公差小于0的等差数列,它的前n项和为![]() ,则( )
,则( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
5. 对![]() ,
,![]() 是数列
是数列![]() 成等差数列的( )
成等差数列的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
6. 已知![]() 为等差数列,公差
为等差数列,公差![]() ,
,![]() ,则
,则![]() ( )
( )
A. 60 B. ![]() C. 182 D.
C. 182 D. ![]()
7. 等差数列![]() 中的前12项的和为
中的前12项的和为![]() ,其中奇数项之和
,其中奇数项之和![]() 与偶数项之和
与偶数项之和![]() 的比为
的比为![]() ,则
,则![]() 的公差
的公差![]() ( )
( )
A. 10 B. 30 C. 5 D. 15
8. 已知1是![]() 和
和![]() 的等比中项,又是
的等比中项,又是![]() 和
和![]() 的等差中项,则
的等差中项,则![]() 的值是( )
的值是( )
A. 1或![]() B. 1或
B. 1或![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
9. 已知数列![]() 的通项公式
的通项公式![]() ,设其前
,设其前![]() 项和为
项和为![]() ,则使
,则使![]() 成立的自然数
成立的自然数![]() ( )
( )
A. 有最小值31 B. 有最大值31 C. 有最小值63 D. 有最大值63
10. 已知数列![]() 满足
满足![]() 且
且![]() ,其前
,其前![]() 项和为
项和为![]() ,则满足不等式
,则满足不等式![]() 的最小整数
的最小整数![]() 是( )
是( )
A. 5 B. 6 C. 7 D. 8
二. 填空题(共5小题,每题4分)
11. 若函数![]() 的定义域是
的定义域是![]() ,则
,则![]() 的定义域是 。
的定义域是 。
12. 函数![]() 的单调递增区间是
。
的单调递增区间是
。
13. 计算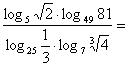 。
。
14. 设![]() 是公比为q的等比数列,
是公比为q的等比数列,![]() 是它的前
是它的前![]() 项和,若
项和,若![]() 是等差数列,则
是等差数列,则![]() 。
。
15. 一辆卡车从工地运20根电线杆到500米外的公路一端开始埋栽,每隔50米埋一根,每次最多运三根,要完成任务并返回工地,卡车总的最短路程是 米。
三. 解答题(共4小题,每题10分)
16. 七个实数排成一列,奇数项成等差数列,偶数项成等比数列,且奇数项之和与偶数项之积的差为42,首项、末项、中间项之和为27,求中间项。
17. 已知函数![]() (其中
(其中![]() ,
,![]() )。
)。
(1)求反函数![]() 及其定义域;
及其定义域;
(2)解关于![]() 的不等式
的不等式![]()
18. 数列![]() 的前n项和为
的前n项和为![]() ,对
,对![]() ,
,![]() 有
有![]() 。
。
(1)求![]() 的通项公式
的通项公式
(2)设![]() ,且
,且![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 。
。
19. 已知等比数列![]() 的各项为不等于1的正数,数列
的各项为不等于1的正数,数列![]() 满足
满足![]() (
(![]() ,且
,且![]() ),设
),设![]() ,
,![]() 。
。
(1)数列![]() 的前多少项和最大,最大值为多少?
的前多少项和最大,最大值为多少?
(2)令![]() (
(![]() ,
,![]() ),试比较
),试比较![]() 与
与![]() 的大小;
的大小;
(3)试判断是否存在自然数![]() ;使得当
;使得当![]() 时,
时,![]() 恒成立,若存在,求出相应的
恒成立,若存在,求出相应的![]() ;若不存在,说明理由。
;若不存在,说明理由。
【试题答案】
一.
1. B
解析: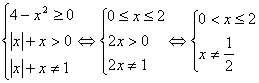
2. C
解析:由![]() 在
在![]() 减,则
减,则![]() 或
或![]()
3. A
解析:利用图形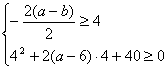
![]()
4. A
解析:![]() 又
又![]() 则
则![]()
由![]() ,
,![]() 故
故![]()
5. A
6. B
解析:由![]()
![]()
![]()
7. C
解析:设![]() 由
由![]()
又![]()
8. D
解析:![]() ,
,![]() 即
即![]() 则
则![]() 或
或![]()
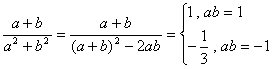
9. C
解析:由![]()
![]()
![]()
![]()
10. C
解析:![]() ,令
,令![]() ,则
,则![]()
![]() 且
且![]() ,故
,故![]() 为首项
为首项![]() ,公比
,公比![]() 的等比数列。
的等比数列。
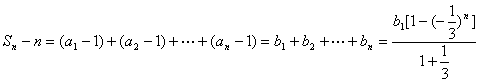
![]() 则
则![]() 满足该不等式的最小整数
满足该不等式的最小整数![]() 。
。
二.
11.
![]()
解析:由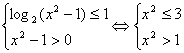
12.
![]()
解析: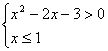
![]()
![]()
13.
![]() 14. 1
14. 1
15. 14000
解析:![]()
三.
16.
解:设奇数项为![]() ,
,![]() ,
,![]() ,
,![]()
偶数项为![]() ,
,![]() ,
,![]()
由已知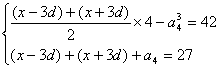
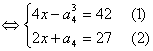
![]() 得
得![]()
![]()
![]()
17. 解:
(1)当![]() 时,由
时,由![]() 得出函数定义域
得出函数定义域![]() ;当
;当![]() 时,由
时,由![]() 得函数定义域为
得函数定义域为![]() 。
。
由![]()
![]() 则
则
![]()
故 当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]()
(2)![]()
![]()
由 ![]() 则原不等式
则原不等式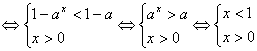
![]()
18. 解:
(1)![]() ,
,![]() 即
即![]() 则
则![]() 两式相减
两式相减![]() 故
故![]()
令 ![]() ,
,![]()
![]()
(2)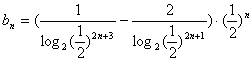
![]()
![]()
故![]()
![]()
![]()
![]()
19. 解:
(1)![]() ,
,![]() ,则
,则![]()
![]()
由![]() 为等比数列,则
为等比数列,则![]() 为定值,故
为定值,故![]() 为等差数列
为等差数列
由![]() ,
,![]()
![]() ,
,![]()
故当![]() 或
或![]() 时,
时,![]() 取最大值且最大值为132。
取最大值且最大值为132。
(2)由![]()
![]()
由 ![]() 在
在![]() 上为减函数,故
上为减函数,故![]()
(3)对![]()
当![]() 时,
时,![]()
![]()
当![]() 时,
时,![]()
故当![]() 时,存在
时,存在![]() ,当
,当![]() 时,
时,![]() 恒成立。
恒成立。
【试卷分析】
本试卷综合考了对数运算、对数函数、数列、等差数列和等比数列等内容,紧扣大纲和教材,在重点考查基础知识的同时,也注重了能力的考查和提高。
| 年级 | 高一 | 学科 | 数学 | 版本 | 期数 | |||||
| 内容标题 | 天津市2003——2004学年度上学期期末高一数学试卷 | |||||||||
| 分类索引号 | G.623.3 | 分类索引描述 | 学习资料 | |||||||
| 主题词 | 天津市2003——2004学年度上学期期末高一数学试卷 | 栏目名称 | 名校题库 | |||||||
| 编稿老师 | 审稿老师 | |||||||||
| 录入 | 孙莹 | 一校 | 李蕾 | 二校 | 孟蕊 | 审核 | ||||