高一数学上学期期末综合测试
【同步达纲练习】
一、选择题：（每小题3分，共36分，每小题有且仅有一个正确答案）
1．集合
则（ ）
A、
B、
C、M=N D、以上答案都不对
2．设角α的终边经过点P（3x，-4x）（x＜0），则sinα-cosα的值为（ ）
A、
B、
C、
D、
3．下列各函数中，在区间（0，1）内为减函数的是（ ）
A、
B、
C、
D、
4．若y=f（x）是奇函数，则y=f（x）是（ ）
A、奇函数 B、既是奇函数又是偶函数
C、偶函数 D、既不是奇函数又不是偶函数
5．直线AB与平面α成50°角，则AB与平面α内不过交点的任一直线所成角的范围是（ ）
A、（0°，90°） B、（50°，90°） C、（50°，90°） D、（0°，50°）
6．下列判断正确的是（ ）
A、直线AB平行于平面M内的直线CD，则AB
平面M
B、平面M内两条直线平行于平面N，则平面M平面N
C、平面M平面N，则平面M内任一直线都平行于平面N
D、直线AB平面M，则直线AB平行于平面M内的任一直线
7．若2弧度的圆心角所对的弧长为4cm，则这个圆心角所夹的扇形的面积是（ ）
A、4
B、2 C、4π D、2π
8．已知A为锐角，lg（1+cosA）=m，lg
，则lgsinA=（ ）
A、
B、
C、
D、
9．若函数f(x)的图象过点(0,1)，则函数y=f(x-3)的反函数的图象必过点（ ）
A、(1,-3) B、(-3,1) C、(1,3) D、(3,1)
10．直角△ABC所在平面为α，两直角边长分别为3和4，平面α外一点P到A、B、C三点的距离都是5，那么点P到平面α距离为（ ）
A、
B、
C、
D、
11．空间四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，若对角线AC=6，BD=8，那么
的值是（ ）
A、200 B、100 C、20 D、10
12．函数y=
上单调递减，则a的取值范围是（ ）
A、
B、
C、
D、
二、填空题（每上题3分，共18分）
13．已知tgα=3，则
______________。
14．函数y=
的单调递减区间是___________________。
15．空间四边形ABCD中，AB=BC=CD=DA=AC=BD，E是AB中点，则AD与CE所成角的余弦值为____________________。
16．正方体ABCD-
的棱长为a，M是CD中点，则异面直线
的距离为_____________________。
17．设a＞0且a≠1，若
＜1，则a的取值范围是____________________。
18．函数
的值域是__________________________。
三、解答题：（共46分）
19．（6分）化简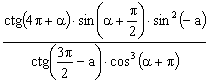
20．（6分）设α是第二象限角，化简
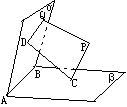
21．（8分）已知平面α∩平面β=AB，PQ⊥α于Q，PC⊥β于C，CD⊥α于D，求证QD⊥AB。
22．（8分）已知：正方体ABCD的边长为4，E为AD上的一点，AE=1，连结EC，M是EC上的一点，过点M作NQBC，MPAB分别交AB于N，交DC于Q，交BC于P，设MQ=x，矩形MNBP的面积为S。
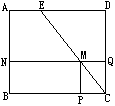
（1）试将S表示为x的函数S=f(x)；（2）求函数S=(x)的定义域和值域。
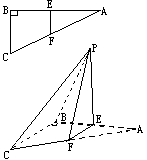
23．（8分）如图，△ABC中，∠ABC=90°，AB=BC=2，E、F分别是AB、AC的中点，以EF为棱把它折起，使A至点P的位置，成直二面角P-EF-B。
（1）求∠PFC的大小；（2）求二面角P-CF-B的正切值。
24．（10分）设f(x)=1-2a-2acosx-2
x的最小值为g(a)(a∈R)。（1）求g(a)的表达式；（2）当g(a)=
时，求a的值及此时f(x)的最大值。
参考答案
一、选择题：（每小题3分，共36分，每小题有且仅有一个正确答案）
1、C 2、A 3、D 4、C 5、B 6、C 7、A 8、D 9、C 10、B 11、C 12、A
二、填空题：（每小题3分，共18分）
13、
14、（-1，2） 15、
16、a 17、a＞2或0＜a＜1 18、
三、解答题：（共46分）
19、（6分）化简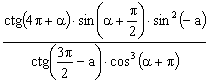
=
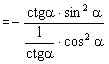
20．（6分）原式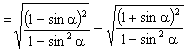
=
∵-1≤sinα≤1 ∴1+sinα≥0， 1-sinα≥0
又∵α是第二象限角 ∴cosα＜0
∴原式=
21．（8分）
证明：∵PQ⊥α，CD⊥α，AB
α
∴PQCD，PQ⊥AB
∴过PQ和CD确是一个平面γ。
∴QDγ，PCγ，PQγ
∵PC⊥β，ABβ
∴PC⊥AB
∴AB⊥γ
∴AB⊥QD
22．（8分）
（1）∵NQBC，NBQC
∴NQ=BC=4
∵MQ=x
∴NM=4-x
∵BCAD
∴MQAD
∴
∵AE=1，AD=4，CD=4
∴ED=3
∴CQ=
x
∵MPAB，ABCD
∴MPCD
又∵MQBC
∴MP=CQ=x
∴S=NM·MP=（4-x）x
即S=
（2）∵M是EC上的一点
∴S的定义域是{x0＜x≤3}
又∵
∴ 0＜S≤
即S的值域是
23．（8分）
（1）∵在△ABC中，AB=BC=2，∠ABC=90°
∴AC=
∵E、F分别是AB、AC中点
∴EFBC，EF=1，BC=2，
AE=EB=1，AF=FC=
∴EF⊥AB
∴折起后，PE⊥EF，PE=BE=1
PF=FC=
又∵平面PEF⊥平面CFEB
∴PE⊥平面CFEB
∴PE⊥EB ∴PB=
∵CB⊥BE，PE⊥平面CFEB
∴CB⊥PB ∴PC=
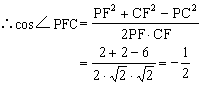
∴∠PFC=120°
（2）过点E作EG⊥CF交CF延长线于G，连结PG
∵PE⊥平面BFE，EG⊥FC
∴PG⊥FC
∴∠PGE是二面角P-CF-B的平面角
∴tg∠PGE=
在△ABC中，∵EF=EA=1，EG⊥CA ∴G是FA的中点
又∵EF⊥EA ∴EG=
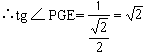
24．（1）f(x)=1-2a-2acosx-2（1-
x）
=1-2a-2acosx-2+2x
=2x-2acosx-2a-1
设t=cosx，则t∈[-1，1]
(t)=2
-2at-2a-1
=2
当
当-1＜
＜1即-2＜a＜2时，
当≥1即a≥2时，
∴
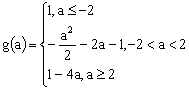
（2）由
得：a=-3或a=-1
又∵-2＜a＜2 ∴a=-3舍去 ∵a=-1
由1-4a=,得a=
又∵a≥2 ∴a=,舍去
∴当g(a)= 时,a=-1
此时,