高一数学第一学期期未教学质量检测试卷5
一、选择题(每小题3分,共36分)
1.如果S={1,2,3,4},M={1,3,4},N={2,4},那么(![]() SM)∩(
SM)∩(![]() SN)=( )
SN)=( )
(A) ![]() (B) {1,3} (C) {4} (D) {2,5}
(B) {1,3} (C) {4} (D) {2,5}
2.如果命题“p或q”与命题“非p”都是真命题,那么( )
(A) 命题p是真命题 (B) 命题q是假命题
(C) 命题p与命题q的真值相同 (D) 命题q是真命题
3.x≤2是x<2的( )
(A) 充分非必要条件 (B) 必要非充分条件
(C) 充要条件 (D)既非充分条件也非必要条件
4.如果a,b,c成等比数列,那么关于x的方程ax2+bx+c=0( )
(A) 一定有两不等实根 (B) 一定有两相等实根
(C) 一定无实根 (D) 有两符号不相同的实根
5.函数y=2x+a的图象不经过第二象限,则( )
(A) a≤0 (B) a≥0 (C) a≤-1 (D)a≥-1
6.设1<a<2<c,则下列不等式中正确的是( )
(A) ![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.等差数列{an}中,已知a1+3a8+a15=120,则a8的值等于( )
(A) -8 (B) 24 (C) 22 (D) 20
8.直线y=1与函数y=![]() 的图象交于A、B两点,则线段AB长为( )
的图象交于A、B两点,则线段AB长为( )
(A) 1 (B) 2 (C) a (D) 2a
9.(普通)若数列{an}前n项和Sn=3n-1,则数列{an}是( )
(重点)若数列{an}前n项的和Sn=an-1(a≠0),则数列{an}是( )
(A) 等比数列 (B) 不是等比数列
(C)可以是等比数列,也可以是等差数列
(D)可以是等比数列,但不可是等差数列
10(普通)在等差数列{an}中,前n项和Sn=36n-n2,则Sn中最大的是( )
(A) S1 (B) S9 (C) S17 (D) S18
(重点)在等差数列{an}中,a1>0,a18+a19=0,则{an}前n项和Sn中最大的是( )
(A) S8 (B) S9 (C) S17 (D) S18
11.(普通)如果等比数列{an}的首项为正数,公比大于1,那么{lgan}是( )
(重点)如果等比数列{an}的首项为正数,公比大于1,那么{lg![]() an}是( )
an}是( )
(A) 递增的等比数列 (B) 递增的等比数列
(C) 递增的等差数列 (D) 递增的等差数列
12.某人从2004年起,每年1月8日到银行新存入a元(一年定期).若年利率为r保持不变,且每年到期存款及利息转为新的一年定期存款,到2009年1月7日将所有存款及利息全部取回(不考虑利息税),他可取回的钱数为( )
(A) a(1+r)5元 (B) ![]() [(1+r)5-(1-r)] 元
[(1+r)5-(1-r)] 元
(C) a(1+r)6元 (D) ![]() [(1+r)6-(1-r)] 元
[(1+r)6-(1-r)] 元
二、填空题(共8小题,每小题3分,共24分.把答案填在题中的横线上)
13.设A={平面M内的圆},B={平面M内的四边形},对应法则:“画圆的内接四边形”,那么从A到B的对应是否映射?_________.(填“是”可“否”).
14.写出函数y=![]() 的一个单调递减区间_________.
的一个单调递减区间_________.
15.方程x2+mx+m-1=0有一正根和一负根,则实数m的取值范围是_________.
16.函数f(x)=-![]() (0≤x≤1)的反函数为_________.
(0≤x≤1)的反函数为_________.
17.函数y=lg(2x+1)的定义域为_________.
18.已知下列三个命题
⑴ “正方形是菱形”的否命题
⑵ “若ac2>bc2,则a>b”的逆命题
⑶ 若m>2,则不等式x2-2x+m>0的解集为R,其中真命题为_________.(请把你认为正确的命题前面序号填在横线上)
19.(普通) 已知f(x)=![]() ,则f(2)+f(
,则f(2)+f(![]() )+f(3)+f(
)+f(3)+f(![]() )=_________.
)=_________.
(重点)已知f(x)=![]() ,则f(2)+f(3)+f(4)+…+f(10)+f(
,则f(2)+f(3)+f(4)+…+f(10)+f(![]() )+f(
)+f(![]() )+…+f(
)+…+f(![]() )=
)=
20.(普通)已知数列{an}中,a1=1,![]() +1(n≥2,n∈N*),则a5=_________.
+1(n≥2,n∈N*),则a5=_________.
(重点)已知f(x)=![]() ,数列{an}满足an=f(
,数列{an}满足an=f(![]() )(n≥2,n∈N*),且a1=1,则a10=_________.
)(n≥2,n∈N*),且a1=1,则a10=_________.
三、解答题(本大题共4小题,满分40分,解答应写出文字说明、证明过程或演算步骤)
21.(本小题满分8分)
(普通)解不等式 ![]() ≤0
≤0
(重点)解不等式![]() ≤0
≤0
22.(本小题满分11分)
设{an}为等比数列,{bn}为等差数列,且b1=0,cn=an+bn,若{ cn}是1,1,2,…….
⑴ 求{an}的公比q和{bn}的公差d;
⑵ 求数列{ cn }的前10项和.
23.(本小题满分10分)
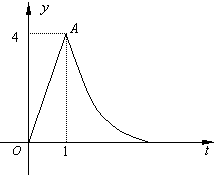 某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(OA为线段,AB为某二次函数图象的一部分,B为原点).
某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(OA为线段,AB为某二次函数图象的一部分,B为原点).
⑴ 写出服药后y与t之间的函数关系式y=f(t);
⑵ 据进一步测定:每毫升血液中含药量不少于![]() 微克时,对治疗有效,求服药一次治疗疾病有效的时间?
微克时,对治疗有效,求服药一次治疗疾病有效的时间?
24.(本小题满分11分)
已知函数f(x)=3x,且![]() (18)=a+2,g(x)=
(18)=a+2,g(x)=![]() .
.
⑴ 求a的值;
⑵ 求g(x)的表达式;
⑶(普通)当x∈[-1,1]时,g(x)的值域并判断g(x)的单调性;
(重点)问是否存在区间A,使得当x∈A时,g(x)的值域为[-2,![]() ]且在A上存在反函数?若存在,求符合条件的一个A,并判断g(x)在A上的单调性,若不存在,说明理由.
]且在A上存在反函数?若存在,求符合条件的一个A,并判断g(x)在A上的单调性,若不存在,说明理由.
第一学期期未教学质量检测
高一数学试卷参考答案及评分标准
一、选择题:(每小题3分,共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | B | C | C | D | B | D | (普)A (重)C | D | (普)C (重)D | D |
二、填空题:(每小题4分,共16分)
13.否
14.(-1,+∞) 或(-∞,-1)(其它也可)
15.(-∞,1)
16.
![]() (x)=
(x)=![]() (-1≤x≤0)
(-1≤x≤0)
17.R
18.⑶
19.(普通) 2
(重点)9
20.(普通) ![]()
(重点)![]()
三、解答题
21.(本题满分8分)
(普通)解:![]() ≤0
≤0![]()
![]() (3分)
(3分)
![]() x≤1或x>
x≤1或x>![]() (6分)
(6分)
∴
原不等式的解集为{x x≤1或x>![]() }.
(8分)
}.
(8分)
(重点)解:![]() ≤0
≤0![]()
![]() (2分)
(2分)
![]() x≤1或x>
x≤1或x>![]()
![]() -1≤x≤1或x>
-1≤x≤1或x>![]() 或x<-
或x<-![]() (6分)
(6分)
∴
原不等式的解集是{x-1≤x≤1或x>![]() 或x<-
或x<-![]() }.(8分)
}.(8分)
22.解:⑴ 依题意,c1=a1+b1=1,
而b1=0,故有a1=1 (2分)
设bn=b1+(n-1)d=(n-1)d (n∈N*)
an=a1•qn-1=qn-1(n∈N*)
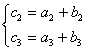 ,即
,即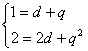 (4分)
(4分)
解得:![]() 或
或![]() ,
,
∵ q≠0,故有![]() (6分)
(6分)
⑵ ∴
an=![]() (n∈N*)
(n∈N*)
bn=1-n(n∈N*) (8分)
c1+c2+…+c10=(a1+a2+…+a10)+(b1+b2+…+b10)
=![]() =210-1-45=978 (10分)
=210-1-45=978 (10分)
∴ 数列{cn}的10项和为978 (11分)
23.⑴ 由已知得y=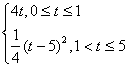 (4分)
(4分)
⑵ 当0≤t≤1时,4t≥![]() ,得
,得![]() ≤t≤1
(6分)
≤t≤1
(6分)
当1<t≤5时,![]() (t-5)2≥
(t-5)2≥![]() ,得t≥
,得t≥![]() ,或t≤
,或t≤![]() ,
,
有1<t≤![]() (8分)
(8分)
∴ ![]() ≤t≤
≤t≤![]() , ∴
, ∴ ![]() -
-![]() =
=![]() .
.
因此,服药一次治疗疾病有效时间为![]() 小时.
小时.
24.解:⑴ ![]() (x)=log3x,log318=a+2,∴
a=log32 (2分)
(x)=log3x,log318=a+2,∴
a=log32 (2分)
⑵
g(x)=![]() (4分)
(4分)
⑶
(普通) 令u=2x,∵ -1≤x≤1,则![]() ≤u≤2,
≤u≤2,
g(x)=![]() (u)=u-u2=-(u-
(u)=u-u2=-(u-![]() )2+
)2+![]() ,
(7分)
,
(7分)
当u=![]() 时,
时,![]() (u)
(u)![]() =
=![]() ,当u=2时,
,当u=2时,![]() (u)
(u)![]() =-2
=-2
∴
g(x)的值域为[-2,![]() ]
(9分)
]
(9分)
当-1≤x≤1时,![]() ≤u≤2,
≤u≤2,![]() (u)为减函数,而u=2x为增函数,
(u)为减函数,而u=2x为增函数,
g(x)在[-1,1]上为减函数 (11分)
(重点) 令u=2x,g(x)=![]() (u)=-(u-
(u)=-(u-![]() )2+
)2+![]() ,
,
g(x)∈[-2,![]() ],∴ -1≤u≤2,而u>0,∴ 0<u≤2
],∴ -1≤u≤2,而u>0,∴ 0<u≤2
为了使g(x)存在反函数,则u∈[![]() ,2],即x∈[-1,1];
,2],即x∈[-1,1];
∴ A=[-1,1] (8分)
当-1≤x≤1时,![]() ≤u≤2,
≤u≤2,![]() (u)为减函数,而u=2x为增函数,
(u)为减函数,而u=2x为增函数,
f(x)在[0,1]上为减函数 (11分)