高一数学第一学期期中考试试卷6
说明:
1. 将选择题及填空题的答案写在答题卡上。
2. 考试时间是120分钟。
一. 选择题:(共10个小题,每小题4分,共40分)
1. 已知集合![]() ,且
,且![]() ,映射
,映射![]() 是从A到B的一个函数,则m、n的值分别是( )
是从A到B的一个函数,则m、n的值分别是( )
A. 2,5 B. 5,2 C. 3,6 D. 6,3
2. 设![]() ,则M、P之间的关系是( )
,则M、P之间的关系是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3. 满足条件![]() 的集合M的个数是( )
的集合M的个数是( )
A. 4 B. 3 C. 2 D. 1
4. 若![]() ,且
,且![]() ,那么
,那么![]() 的值是( )
的值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5. 已知函数![]() 的定义域是[1,2],则函数
的定义域是[1,2],则函数![]() 的定义域是( )
的定义域是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6. 给出下列四个命题:
(1)若![]() ,则
,则![]() 或
或![]() ;
;
(2)若![]() ,则
,则![]() ;
;
(3)若![]() ,则
,则![]() ;
;
(4)![]() ,若
,若![]() 是奇数,则x,y中一个是奇数,一个是偶数。
是奇数,则x,y中一个是奇数,一个是偶数。
则下列说法正确的是( )
A. (4)的逆命题为假 B. (1)的逆命题为真
C. (2)的否命题为真 D. (3)的否命题为假
7. 经过统计知:某村有电话的家庭35家,有农用三轮车的家庭65家,既有电话又有农用三轮车的家庭有20家,则电话和农用三轮车至少有一种的家庭数为( )
A. 60 B. 80 C. 100 D. 120
8. 下列函数中值域是![]() 的是( )
的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
9. 已知函数![]() 满足
满足![]() 且
且![]() ,那么
,那么![]() 等于( )
等于( )
A. 36 B. 10 C. 5 D. 18
10. 在如图的电路图中,闭合开关A是灯泡B亮的( )条件。
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
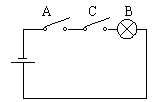
二. 填空题:(共4个小题,每小题4分,共16分)
11. “p或q”为真命题是“p且q为真命题”的________________条件。
12. 若函数![]() 在区间
在区间![]() 上单调递减,则实数m的取值范围是__________________。
上单调递减,则实数m的取值范围是__________________。
13. 已知函数![]() 定义域为
定义域为![]() ,则函数
,则函数![]() 的定义域为____________。
的定义域为____________。
14. 若![]() ,则
,则![]() _________,
_________,![]() 的化简结果是________。
的化简结果是________。
三. 解答题(共6个小题,共44分)
15. (满分7分)
解不等式:![]()
16. (满分7分)
设集合![]() ,若
,若![]() ,求实数p的取值范围。(说明:
,求实数p的取值范围。(说明:![]() 表示正实数集)。
表示正实数集)。
17. (满分7分)
设函数![]()
(I)判断函数![]() 在R上的奇偶性;
在R上的奇偶性;
(II)用定义证明函数![]() 在
在![]() 上是增函数。
上是增函数。
18. (满分8分)
已知全集![]() ,若
,若
![]() ,
,![]() ,求实数c的取值范围。
,求实数c的取值范围。
19. (满分8分)
已知在R上定义的函数![]() 满足:
满足:![]() ,
,
(1)求![]() ;
;
(2)若方程:![]() 有两个实数根
有两个实数根![]() ,且
,且![]() ,求m的取值范围。
,求m的取值范围。
20. (满分7分)
某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高一元,将有3张床位空闲。为了获得较好的经济效益,该宾馆要给每张床位定一个合适的价格。条件是:①要方便结帐,床位价格应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且是越高出的多越好。
若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)。
(1)把y表示成x的函数,并求出其定义域。
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入最多。
【试题答案】
一. 选择题:(共10个小题,每小题4分,共40分)
1. B 2. D 3. C 4. A 5. A
6. B 7. B 8. C 9. B 10. B
二. 填空题:(共4个小题,每小题4分,共16分)
11. 必要不充分条件
12. ![]()
13. ![]()
14. ![]()
三. 解答题:(共6个小题,共44分)
15. (满分7分)
解不等式:![]()
解:原不等式化为:![]()
即: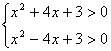 ,解得:
,解得: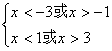
所以原不等式的解集是![]()
16. (满分7分)
设集合![]() ,若
,若![]() ,求实数p的取值范围。(说明:
,求实数p的取值范围。(说明:![]() 表示正实数集)。
表示正实数集)。
解:由方程![]() 知,
知,
![]()
(1)![]() ,则
,则![]() ,此时
,此时![]() ;
;
(2)若![]() ,则
,则![]() 或
或![]() 时,
时,
设![]() 为
为![]() 的两个实根
的两个实根
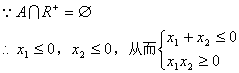
由于![]() 恒成立,
恒成立,
![]()
![]() 解得:
解得:![]()
故有:![]()
所以由(1)(2)可知,p的取值范围是![]() 。
。
17. (满分7分)
设函数![]()
(I)判断函数![]() 在R上的奇偶性;
在R上的奇偶性;
(II)用定义证明函数![]() 在
在![]() 上是增函数。
上是增函数。
解:(1)![]() 是奇函数,这是由于
是奇函数,这是由于![]()
![]()
∴函数![]() 是奇函数
是奇函数
(2)设![]() 且
且![]() ,则:
,则:
![]()
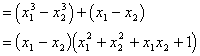
![]()
而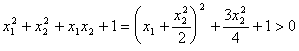 恒成立
恒成立
![]() ,即
,即![]()
故根据单调增函数的定义,函数![]() 在
在![]() 上是增函数
上是增函数
18. (满分8分)
已知全集![]() ,若
,若
![]() ,
,![]() ,求实数c的取值范围。
,求实数c的取值范围。
解:依题可知:![]()
![]() 2和3为方程
2和3为方程![]() 的二根,且
的二根,且![]() ,
,
![]() 根据根与系数的关系,得:
根据根与系数的关系,得: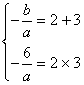
![]()
![]()
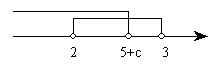
又![]()
![]()
解得:![]()
19. (满分8分)
已知在R上定义的函数![]() 满足:
满足:![]() ,
,
(1)求![]() ;
;
(2)若方程:![]() 有两个实数根
有两个实数根![]() ,且
,且![]() ,求m的取值范围。
,求m的取值范围。
解:(1)设![]() ,则
,则![]()
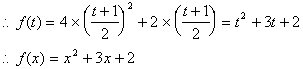
(2)由![]() ,得:
,得:
![]()
![]() 方程有两个实根,
方程有两个实根,![]()
设![]()
当![]() 时,由已知:
时,由已知:![]() ,
,
![]() ,即
,即![]()
当![]() 时,由已知
时,由已知![]()
![]() ,即
,即![]() (舍去)
(舍去)
故![]()
20. (满分7分)
某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高一元,将有3张床位空闲。为了获得较好的经济效益,该宾馆要给每张床位定一个合适的价格。条件是:①要方便结帐,床位价格应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且是越高出的多越好。
若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)。
(1)把y表示成x的函数,并求出其定义域。
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入最多。
解:(1)由题意可得:
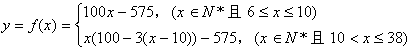
(2)当![]()
当![]()
故当![]() 时,y取最大值,但由于x只能取整数,所以当定价为租金22元时,宾馆的收益最多。
时,y取最大值,但由于x只能取整数,所以当定价为租金22元时,宾馆的收益最多。
| 年级 | 高一 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 北京师大附中2003—2004学年度第一学期期中考试——数学试卷 | ||||||||||||
| 分类索引号 | G.624.6 | 分类索引描述 | 考试试题与题解 | ||||||||||
| 主题词 | 北京师大附中2003—2004学年度第一学期期中考试——数学试卷 | 栏目名称 | 名校题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 李红英 | 一校 | 康纪云 | 二校 | 审核 | ||||||||