试卷类型:A
高一数学调研测试题A
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟.
第 Ⅰ 卷 (选择题,共60分)
注意事项:
1.请考生将自己的姓名、学号、班级填写在第Ⅱ卷的密封线内.
2.每小题选出答案后在第Ⅱ卷前的答题栏内用2B铅笔把对应题目的答案代号涂黑,不能答在试题卷上.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
y = sin2x+![]() cos2x-1的最小正周期是
cos2x-1的最小正周期是
A.4![]() B.2
B.2![]() C.
C.![]() D.
D.![]()
3.
化简![]() 的结果是
的结果是
A.0 B.![]() C.
C.![]() D.
D.![]()
4.
下列函数中,是奇函数的是
A.![]() B.
B.![]() C.y = 2x + 1 D.
C.y = 2x + 1 D.![]()
5.
已知数列{an}的通项公式是an = 2n-39(n∈N*),则Sn取最小值时,n的值为
A.17 B.18 C.19 D.20
6.
已知P1 (2,-1),P2 (0,5),且点P在P1P2的延长线上,使|P1P|= 2|PP2|,则点P的坐标为
A.(-2,11) B.(![]() ,3) C.(
,3) C.(![]() ,3) D.(2,-7)
,3) D.(2,-7)
7.
函数![]() 的单调递增区间是
的单调递增区间是
A.(2,+∞) B.(-1,1) C.(1,+∞) D.(-∞,1)
8.
下列命题中,是真命题的是
A.如果|a|=|b|,那么a = b
B.如果a、b、c是任意向量,那么(a · b) · c
= (b
· c) · a
= (c
· a) · b
C.如果a · b
= a
· c,那么b = c
D.如果向量a和b反向,那么|a-b|=|a|+|b|
9.
将函数![]() (
(![]() >0)的图象C按向量a (a≠0)平移后所得图象仍然为C,则向量a等于
>0)的图象C按向量a (a≠0)平移后所得图象仍然为C,则向量a等于
A.![]() B.
B.![]() (n∈Z且n≠0)
(n∈Z且n≠0)
C.![]() (n∈Z且n≠0) D.
(n∈Z且n≠0) D.![]() (n∈N)
(n∈N)
|
|
10. 函数y = sin x · cot x (0<x<![]() )的大致图形为
)的大致图形为
11. 若e1、e2是单位向量,e1、e2的夹角为60°,则2e2-e1与e1的夹角是
A.30° B.45° C.60° D.90°
12. 函数![]() 图象的一条对称轴是
图象的一条对称轴是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
调研测试题A
高 一 数 学
第 Ⅱ 卷 (非选择题,共90分)
注意事项:
第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中,答卷前将密封线内的项目填写清楚.
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二.填空题:本大题共4小题,每小题4分,共16分.将正确答案填在题中横线上.
13. 在等差数列{an}中,a1+a4+a7 = 15,a3+a6+a9 = 3,则S9 = .
14.
在△ABC中,a、b、c分别是角A、B、C的对边,若a=3![]() ,c=2,B=150°,则b= .
,c=2,B=150°,则b= .
15.
设函数![]() ,则满足
,则满足![]() 的x值为 .
的x值为 .
16.
已知方程![]() 在[0,
在[0,![]() ]内有两不相等的实根,则常数a的取值范围是 .
]内有两不相等的实根,则常数a的取值范围是 .
三.解答题:本大题共6小题,满分74分.
| 得分 | 评卷人 |
|
|
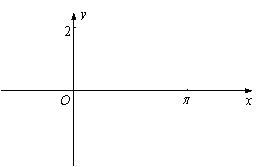
17. (本大题满分12分)已知设O、A、B、C是平面内互异的四个点,且![]() ,确定△ABC的形状.
,确定△ABC的形状.
| 得分 | 评卷人 |
18.
 (本大题满分12分)已知函数
(本大题满分12分)已知函数![]()
![]()
(1)用“五点法”作函数在长度为一个周期的闭区间上的图象;
(2)求函数的最大值和最小值;
(3)指出函数的单调递增区间.
19.
(本大题满分12分) 在△ABC中,![]() ,
,![]() ,且最长边的长为1,求:
,且最长边的长为1,求:
(1)角C的大小;
(2)△ABC的最短边的长.
| 得分 | 评卷人 |
20.
(本大题满分12分) 已知![]() ,
,![]() ,求值:
,求值:
![]() .
.
| 得分 | 评卷人 |
21.
(本大题满分12分)已知函数![]() (a≠0),x∈[0,
(a≠0),x∈[0,![]() ]时,f (x)的值域为[-5,1],求a、b的值.
]时,f (x)的值域为[-5,1],求a、b的值.
| 得分 | 评卷人 |
22. (本大题满分14分)已知a=(3,-4),a+b=(4,-3).
| 得分 | 评卷人 |
(1)求向量a与b的夹角![]() ;
;
(2)对两个向量p和q,如果存在不全为零的常数![]() ,使
,使![]() ,则称向量p、q是线性相关的,否则称之为线性无关的.问:向量a、b是线性相关还是线性无关的?
,则称向量p、q是线性相关的,否则称之为线性无关的.问:向量a、b是线性相关还是线性无关的?
高一数学参考答案及评分标准
一.选择题:ACDDC AADCB DA
二.填空题:13.27 14.7 15.3 16.{a|-2<a≤-![]() }
}
三.解答题:
17.解:![]() 3分
3分
![]() 6分
6分
∵![]()
∴![]()
即![]() 10分
10分
∴△ABC是等腰三角形. 12分
| x |
|
|
|
|
|
|
| 0 | 2 | 0 | -2 | 0 |
18.解:![]()
![]() 4分
4分
6分
图略 8分
当![]() ,即
,即![]() (k∈Z)时,函数的最大值为2,
(k∈Z)时,函数的最大值为2,
当![]() ,即
,即![]() (k∈Z)时,函数的最小值为-2 10分
(k∈Z)时,函数的最小值为-2 10分
函数的单调递增区间是![]() (k∈Z) 12分
(k∈Z) 12分
19.(1)解:∵![]() ,
,![]() ,A+B+C = 180°
,A+B+C = 180°
∴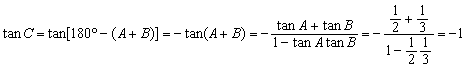
∴C = 135°. 6分
(2)解:由tan A>tanB>0知A>B且A、B是锐角,故C>A>B
∴b是最短边,c是最长边 8分
由![]() 得:3sin B = cos B,又sin2B+cos2
B = 1
得:3sin B = cos B,又sin2B+cos2
B = 1
∴10sin2B = 1 Þ ![]() 10分
10分
由正弦定理得: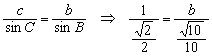
∴![]() ,即三角形的最短边的长为
,即三角形的最短边的长为![]() . 12分
. 12分
20.解:∵![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() 4分
4分
∴![]()
![]() 6分
6分
Þ ![]() 8分
8分
∴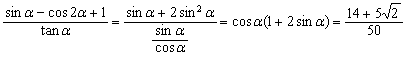 12分
12分
21.解:![]() 4分
4分
∵x∈[0,![]() ],∴
],∴![]()
∴![]() 8分
8分
当a>0时,b≤f (x)≤3a+b,故![]() 10分
10分
当a<0时,3a+b≤f (x)≤b,故![]() 12分
12分
22.(1)解:∴a=(3,-4),a+b=(4,-3) ,∴b = (1,1)
∴![]() 4分
4分
∵0≤![]() ≤
≤![]() ,∴
,∴![]() 7分
7分
(2)解:若向量a与b是线相关的,则存在不全为零的常数![]() ,使
,使![]() ,
,
即![]() 9分
9分
∴![]() 12分
12分
与![]() 不全为零矛盾
不全为零矛盾
因此向量a与b是线性无关的.
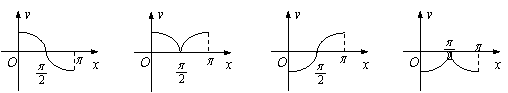 A B C D
A B C D