高一数学寒假作业

高一数学寒假作业（一）

一、选择题（共 12 小题，每小题 5 分，共 60 分）

1、设S为全集，A、B为非空集合，且，则下列集合为空集的是 （ ）

A．　　　　　　　　　B．

C．　　　　　　　D．

2、命题p：(x－1)(y－2)=0，命题q:(x－1)2＋(y－2)2=0，命题p是命题q的 （ ）

A．充分不必要条件　　　　　 B．必要不充分条件

C．充分必要条件　　　　　　 D．既不充分也不必要条件

3、设集合M={－1，0，1}，N={2，3，4}，从M到N的映射f满足条件：对每一个x∈M，都有x＋f(x)为偶数，那么这样的映射个数为（ ）

A．2　　　　　　　　　　　　B．8

C．9　　　　　　　　　　　　D．27

4、不论a为何值时，函数恒过一定点，则这个定点的坐标是 （ ）

A．　　　　　　　　　B．

C．　　　　　　　　D．

5、函数f(x)=10x－1－2,则f－1(8)= （ ）

A．2　　　　　　　　　　　　B．4

C．8　　　　　　　　　　　　D．12

6、若1＜x＜2，a=loga22x,b=log2x2,c=log2(log2x),则 （ ）

A．a＜b＜c　　　　　　　　　B．b＜c＜a

C．c＜a＜b　　　　　　　　　D．c＜b＜a

7、设f(x)=2x , g(x)=4x ，且 g[g(x)]＞g[f(x)]＞f[g(x)]，则x的取值范围是 （ ）

A．（-∞,0）　　　　　　　　B．(0,1)

C．(1,+ ∞)　　　　　　　　 D．(-∞,1)

8、已知y=f(x)为增函数，其中 则 （ ）

A．b＞c＞a　　　　　　　　　B．c＞b＞a

C．c＞a＞b　　　　　　　　　D．a＞b＞c

9、设y=f(x)的图象为c1，图象c2与c1关于直线y=x对称，又图象c3与c2关于原点对称，则图象c3所对应的函数是 （ ）

A．y=－f(x)　　　　　　　　 B．y=－f(－x)

C．y=－f-1(x)　　　　　　　 D．y=－f-1(－x)

10、在区间（-∞,0）上为增函数的是（ ）

A．　　　　　 B．

C．y=－(x＋1)2　　　　　　　D．y=1＋x2

11、函数y=4x2－4mx＋m2－2m＋2(m∈ R)在区间[0，2]上的最小值是3，则m等于（ ）

A．　　　　　　　　　　 B．

C．　　　　　　　　 D．

12、某工厂由于生产成本不断降低，产品价格每隔3年降低，已知现在产品价格是6400元，则12年后的产品价格为 （ ）

A．2700元　　　　　　　　　 B．2100元

C．2025元　　　　　　　　　 D．1250元

二、填空题：（每小题 4分，共16分）

13、已知，则f(5)=_________.

14、函数,则函数f-1(2x－x2)的单调递增区间是_________.

15、设P=(log2x)2＋(t－2)log2x－t＋1，当t∈[-2,2]时，恒有P＞0，则x的取值范围是_________.

16、如图1所示，ABCD是四边形，动点P沿折线BCDA由B点向A点运动.设P点移动的路程为x，△ABP的面积为S，函数S=f(x)的图象如图2所示，给出以下四个结论．

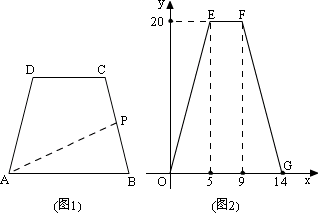
（1） ABCD 是等腰梯形，且 AB∥CD ；

（2） ABCD 是平行四边形；

（3） Q 是 AD 的中点，△ABQ 的面积为 10 ；

（4）当 10 ≤x ≤ 14 时，函数 S=f(x) 的解析式是 f(x)=56－4x ；其中正确命题的序号是 _________ （把你认为正确的序号都填上 . ）

三、解答题（满分 74 分）

17 、（本小题 12 分）设命题为“若 m ＞ 0 ，则关于x 方程x2 ＋x－m=0 有实数根”，试写出它的逆命题，否命题和逆否命题，并分别判断它们的真假 .

18 、（本小题 12 分）求函数在区间（ -∞,2]上的值域.

19 、（本小题 12 分）已知函数 f(x) 在 [0 ，＋ ∞）上是减函数，且 f(x)≠0,f(2)=1，试判断在区间[0，2]上的增减性，并加以证明.

20、（本小题满分12分）生产某种产品x吨，所需费用是元，当出售这种商品x吨时，每吨价格为P元，其中(a、b是常数)，如果生产出来的这种商品能够全部卖完，那么当产量是150吨时，利润最大，并且这时每吨的价格是40元，求a、b的值.

21、（本小题12分）（1）求函数（a＞0，且a≠1）的定义域.

　　　　　　　　　（2）已知f(x)的定义域为[0，1]，求的定义域.

22、（本小题14分）已知函数f(x)=x2－(m＋5)x＋2(m＋5)在其定义域内恒为非负，求方程的根的取值范围.

答案：

一、1．Ｃ，２．Ｂ，３．Ａ，４．Ｃ，５．Ａ，６．Ｃ，７．Ｂ，８．Ｄ，９．Ｄ，１０．Ｂ，１１．Ｄ，１２．Ｃ

二、１３、８，１４、[1，2），１５、，１６、①③④

三、１７、解答：逆命题为：若关于x的方程x²＋x－m=0有实数根，则m＞0，这是一个假命题.

　否命题为：若 m≤0，则关于x的方程x²＋x－m=0没有实数根，此命题为假.

　逆否命题：若关于x的方程x²＋x－m=0的无实根，则m≤0此命题为真.

１８、解答： 本题主要考换元思想，配方法等 .

　令 u=2^x，则

　∵x≤2,∴0＜u≤4，∴f(3)≤f(u)＜f(0)

　即,故函数值域为.

１９、解答：

　　　本题是利用抽象函数考查单调性概念及不等式知识等 .两个单调性不同的函数相加产生的和函数单调性，需从定义出发去判断.

　F(x)在[0,2]上是减函数.设0≤x₁＜x₂≤2，则

　

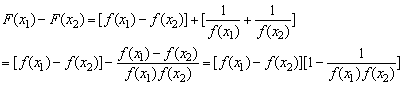
　∵ f(x)在[0，+∞)上是减函数，且f(2)=1,

　∴ f(x₁)－f(x₂)＞0，且f(x₁)＞1, f(x₂)≥1,

　故 f(x₁)f(x₂)＞1,∴,即F(x₁)＞F(x₂),

　所以 F(x)在[0,2]上是减函数.

２０、解答： 本题主要考查二次函数最大值问题及用所学数学知识解决实际问题的能力 .

　当x=150时，P=40，即　　　　　　 ①

　当出售x吨时，利润为y元，则

　

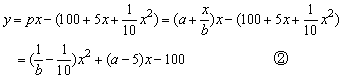
　由①，②中消 b得：

　

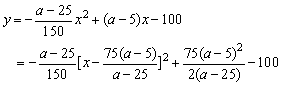
　∴ 当时，y有最大值.

　将x=150代入得a=45，这时b=-30.

２１、解答：本小题主要考查定义域概念，基本的对数不等式知识及函数记号的理解、分类思想 .

（1）∵1－log_a(x＋a)＞0，即log_a(x＋a)＜1，当 a＞1时，0＜x＋a＜a,

∴ 函数定义域为(-a,0)，当0＜a＜1时，x＋a＞a，

∴ 函数定义域为（0,+∞）.

（2）∵f(x)的定义域为[0，1]，∴欲使函数有意义，必须满足

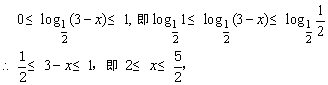
所以函数的定义域为 [2，].

２２、解答：本小题融二次函数，指数函数及绝对值知识于一体，综合考查考生的整体素质 .

　由题意得△=(m＋5)²－4×2×(m＋5)≤0,

　即 (m＋5)(m－3)≤0, 解之得 -5≤m≤3.

　当 -5≤m≤2时，原方程变为：2^x =(m＋1)[1－(m－2)]

　即 2^x =－(m－1)²＋4，所以0＜2^x ≤4，此时,1＜x≤2；

　当 2≤m≤3时，原方程变为2^x =(m＋1)(m－2＋1)=m²－1，

　∴ 3≤2^x ≤8，此时，log₂3≤x≤3．