高一数学测试题—平面向量的坐标运算(7)
一、选择题:
1、已知A(2,1),B(3,2),C(-1,4),则ΔABC是 ( )
A.锐角Δ B.Rt Δ C.钝角Δ D.任意Δ
2、已知a=(-3,4), b=(4,-3), 则a b 等于 ( )
A.0 B.25 C.-24 D.24
3、已知a=(2,3) ,b=(-4,7) ,则a在b上的投影值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知a=(2,1) , b =(3,x), 若(2a-b)⊥b,则x的值为 ( )
A.3 B.-1 C.-1或3 D.-3或1
5、A(0,-3)、B(3,3)、C(x,-1),且![]() ∥
∥![]() 则x等于 ( )
则x等于 ( )
A.5 B.1 C.-1 D.-5
6、若向量a = (1,1), b= (1,-1), c =(-1,2),则 c 等于 ( )
A.-![]() a+
a+![]() b B.
b B.![]() a-
a- ![]() b C.
b C.![]() a-
a- ![]() b D.-
b D.- ![]() a+
a+ ![]() b
b
7、已知a=(4,2), b= (6,y)且 a∥b,则y的值为 ( )
A.2 B.3 C.4 D.5
8、若向量a=(1,-2) , b = 4 a,且a,b共线,则b可能是 ( )
A.(4,8) B.(-4,8) C.(-4,-8) D.(8,4)
二、填空题:
9、已知a=(3,4) ,b⊥a且b的起点为(1,2),终点为(x,3x), 则b=_______.
10、已知a=(2,4), b=(-1,-3),c=(-3,2). 则3a+2b=________. 若一个单位向 量u与a-c的方向相同,则u的坐标为________________.
11、已知a=(2,-1), b=(λ,3).
1)若a与b的夹角为锐角,则λ的取值范围是________.
2)若a与b的夹角为钝角,则λ的取值范围是_________.
3)若a⊥b,则λ的取值范围是_________.
4)若a∥b,则λ的取值范围是_________.
12、在平行四边形ABCD中,已知AB=4,AD=3,∠DAB=60°,则![]() ·
·![]() =___
____,
=___
____, ![]() ·
·![]() =_______.
=_______.
三、解答题:
13、平面向量a = (3,-4), b= (2,x), c=(2,y),已知a∥b,a⊥c,求b,c及b,c的夹角.
14、已知向量a= (4,3), b=(-1,2),
①求a、b的夹角; ②若向量a-λb与2a+b垂直,求λ的值.
15、试证三角形的三条高线交于一点.
16、设向量![]() =(3,1) ,
=(3,1) , ![]() =( -1,2),向量
=( -1,2),向量 ![]() ⊥
⊥![]() ,
, ![]() ∥
∥![]() ,
,
又 ![]() +
+ ![]() =
= ![]() ,求
,求 ![]() .
.
高一数学测试题—参考答案
平面向量的坐标运算
一、BCCCB BBB
二、(9)![]() (10)
(10)![]() (11)1)
(11)1)![]() 2)
2)![]() ,且
,且![]()
3)![]() 4)
4)![]() (12)9,-6
(12)9,-6
三、(13)分析:先求出x,y,得出b,c后b,c的夹角也容易求得.
解:![]()
![]()
![]() ,
,![]() .
.
![]() 的夹角为90°.
的夹角为90°.
(14)解:①![]() ,
,
![]()
②![]() 与2a+b垂直,
与2a+b垂直,![]() ,又
,又![]() ,
,
![]() ,解得
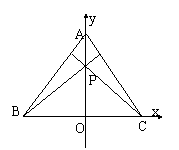
,解得![]() .(15)分析:此题可利用数形结合的办法,通过建立直角坐标系,将几何图形数字化,则问题解决更简洁、更易接受. 证明:设△ABC的BC、CA两边上的高交于P点,现分别以BC、PA所在的直线为x、y轴,建立直角坐标系(如图)
.(15)分析:此题可利用数形结合的办法,通过建立直角坐标系,将几何图形数字化,则问题解决更简洁、更易接受. 证明:设△ABC的BC、CA两边上的高交于P点,现分别以BC、PA所在的直线为x、y轴,建立直角坐标系(如图)
设![]() ,
,
![]()
而![]()
![]()
![]() 是AB上的高. 故△ABC的三条高线交则于一点P.
是AB上的高. 故△ABC的三条高线交则于一点P.
注:两个非零向量的数量积是否为零,是判断相应两条直线是否垂直的重要方法之一.这是典型的转化思想的渗透. (16)![]()
![]()
![]()
又设![]()
![]()
![]() ……① 又
……① 又![]()
![]() ,于是有
,于是有![]() 代入①得k=5,
代入①得k=5,![]()
![]() . 注:也可以直接设
. 注:也可以直接设![]()