高一数学测试题—三角函数的图像和性质（3）

高中学生学科素质训练

高一数学测试题—三角函数的图像和性质（3）

一、选择题：

1、若f(x) cos 是周期为2的奇函数,则f(x)可以是　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 　A．sin 　　　　　B．cos 　　　　C．sinπx　　　　　　D．cosπx

2、把函数y=cos(x + )的图象向右平移φ个单位,所得到的图象正好是关于y轴对称,则φ的最小正值是　　　 （　　）

　　　 A．　　　　  　B．　　  　　　　　 C．　　　　　　　　 D．　

3、函数y=sin(2x +  )的一条对称轴为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 　A．x=　　 　　　　 B．x= 0　　 　　　　　 C．x=－　　  　　D．x =　　

4、方程sinx = lgx的实根有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．1个　　  　　　　 B．3个　　　　 　　C．2个　　　　　　　D． 无穷多个

5、函数y = sin2x+acos2x的图象关于直线x=－ 对称,则a的值为　　　　　　　　　　　　（　　）

　 　A．1　　　　　　 B．－　　　　　　 C．－1 　　　　　　　　　 D．　　

6、已知函数y=f(x),将f(x)图象上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,然　　  后把所得到的图象沿x轴向左平移个单位,这样得到的曲线与y=3sinx的图象相同,　　　那么y=f(x)的解析式为　 （　　）

　 　A．f(x)=3sin()　　　　　　　　 B．f(x)=3sin(2x+)

　 　C．f(x)=3sin( )　　　　　　  　　D．f(x)=3sin(2x－)

7、y= logsin(2x +)的单调递减区间是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 　A．[kπ－,kπ](k∈Z) 　　　　　　　　　　B．(kπ－ ,kπ+ )(k∈Z)

　　　 C．[kπ－ ,kπ+ ] (k∈Z)　　　 D． (kπ－, kπ+)(k∈Z)

8、已知y=Asin(ωx+φ)在同一周期内,x=时有最大值, x = 时有最小值－ ,则函数的解析式为　 （　　）

　 　A．y=2sin()　　　　　　　　　　　　　　B．y=sin(3x+ )

　　　 C．y=sin (3x— )　　　　　　　　　　　　　　D．y= sin(3x－ )

二、填空题：

9、已知函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的两个相邻最值点为( ,2), (,－2),则这个函数的解析式为y =____________.

10、设a= logtan70°, b=logsin25°,c=()^cos25°,则它们的大小关系为_________.

11、已知函数y＝2cosx(0≤x≤2π)的图象和直线y＝2围成一个封闭的平面图形，则其面积为＿＿＿＿.

12、下列说法正确的是（填上你认为正确的所有命题的代号）＿＿＿＿。

　 ①函数y＝－sin(kπ＋x)(k∈Z)的奇函数；

　 ②函数y＝sin(2x＋)关于点(  ,0)对称；

　 ③函数y＝2sin(2x＋)＋sin(2x－)的最小正周期是π；

　 ④△ABC中，cosA＞cosB的充要条件是A＜B；

　 ⑤函数＝cos²x＋sinx的最小值是－1

三、解答题：

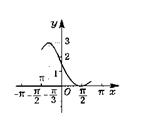
13、已知函数y=Asin(ωx+φ)+b(A>0,φ<π,b为常数)的 一段图象(如图)所示.

　　①求函数的解析式；

　　②求这个函数的单调区间.

 

14、已知a>0,函数y=－acos2x－asin2x+2a+b,x∈[0,].若函数的值域为[－5,1], 求常数a,b的值.

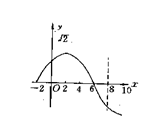
15、己知一条正弦函数的图象,如图所示.

　　①求此函数的解析式；

　　②求与f ₁(x)图象关于直线x=8对称的函数解析式f ₂(x)；

　　③作出y=f₁(x)+f₂(x)的简图.

　　　　　　　　　 

16、如图，扇形OAB的半径为1,圆心角,四边形PQRS是其内接矩形,当矩形面积最大时,求P点位置，并求此时矩形的面积.

　　　　　　　　　　　　　　　　　 

高一数学测试题—参考答案

三角函数的图象和性质

一、ABDBC　 DBB

二、（9）　（10）a<c<b　 （11）4π　　（12）①③④⑤

三、（13）①，

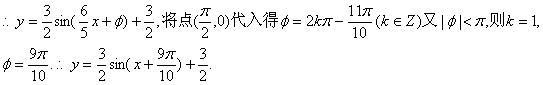
②

是单调递增区间，

（15）①

③]