高一数学测试题—实数与向量的积（5）

高一数学测试题—实数与向量的积（5）

一、选择题：

1、下面给出四个命题：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

1)对于实数m和向量a,b恒有：m(a－b)=ma－mb；

2)对于实数m,n和向量a,恒有：(m－n)a=ma－na；

3)若ma=mb(m∈R)，则有：a=b；

4)若ma=na(m,n∈R,a≠0),则m=n.

其中正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．1　　　 　　　　　　B．2　　　　　  　 C．3　　　　 　　　　D．4

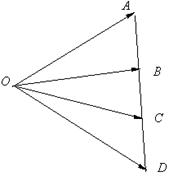
2、设e₁、e ₂是两个不共线的向量，则向量a=e₁+λe₂(λ∈R)与向量b=－(e₂－2e₁)共线的充要条件是　　 （　　）

　　　 A．λ=0　　　 　　　B．λ=－1　　　 　 C．λ=－2　　　　 D．λ=－　　 

 3、设O是菱形ABCD的两对角线交点，下列向量组：　　　　　　　　　　　　　　　　　　　　　（　　）

　　 ①与;　② 与　　 ③  与　 ④ 与  其中可作为这个菱形所在平面表示它的所有向量基底的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．①②　　　　　　 B．③④　　　　  　C．①③　　　　　　　　D．①④

4、己知向量e₁,e₂不共线,下列各项中向量a、b不共线的是　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．a=3e₁, b=5e₂　　　　　　　　　　 　B．a=3e₁, b=6e₂

　　　 C．a=e₁+3e₂,　b=3e₁+9e₂ 　　　　　　　D．a= e₁－e ₂ ,　b=2e₁－4e₂

5、若向量方程2x－3(x－2a)=0,则向量x 等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．a 　　　　　B．－6a　　　　 　　C．6a　　　　　  D．－a

A　　　　　　　　　　  D 　　　　  　　　 O B　　　　　　　　　　　 C

6、在矩形ABCD中，若 =3a, =2b, 则等于　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．(3a+2b)　　　B． (3a－2b)　　　

　　　 C． (2b－3a)　　 D． (3b+2a)　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

7、下列各式或命题中：　　　　　　　　　　　　　　　　　　　　　 

①　－= 　 ②  +  =0  ③　0·=0　 ④若两个非零向量a、b

满足 a=kb(k≠0)，则a、b同向. 正确的个数为　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．0　　　　　　　　　　B．1　　 　　　　　　　　C．2　　　　　　　　　　 D．3　

8、已知O是△ABC内一点,存在一组正实数λ₁,λ₂,λ₃,使λ₁OA +λ₂OB +λ₃OC= 0 ,则∠AOB,∠BOC,∠COA　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．都是钝角　　 　 B．至多有两个钝角　C．恰有两个钝角　D．至少有两个钝角

二、填空题：

9、已知向量a=  i－3j,　b=5i－j,则4a－3b=_____________.

10、己知平行四边形ABCD中， = a , = b, 则 =_______,　=_________.

11、 己知e₁,e₂是不共线的向量，a=ke₁－8e₂,　b=2e₁－ke₂,且a、b共线，则k=____.

12、在正六边形ABCDEF中，己知= a, = b　,则=__________,  =____　　　  ______,　=_________.

三、解答题：

13、设e₁,e₂是两个不共线的向量，则向量b=e₁+λe₂(λ∈R)与向量a=2e₁－e₂共线的　　　　充要条件是什么？

14、如图.C、D是△AOB中边AB的三等分点，试用 = e₁,  = e₂为基底表示　　, .

　　　　　　　　　　　 

15、己知菱形ABCD的对角线交于O,设  = e₁,  =e₂,　= e₃,  =e₄.

　　①试以e₁,e₂为基底表示 、 、 、 ；

　　②以e₁,e₃为基底表示 、 ；

　　③以e₃,e₄为基底表示 、 .

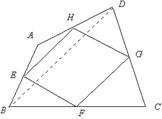
16、用向量的方法证明：顺次连结任一四边形各边中点所得的四边形为平行四　　　　　　　  边形.

　　　　　　　　　　　 

　　　　　　　　　　　　 

高一数学测试题—参考答案

实数与向量的积

一、CDCBC　 AAD

二、（9）　（10）　 （11）　 （12）

三、（13）分析：根据两个共线的充要条件. 即存在实数ub，从而解出.解：a与b共线，

注：在此题中，反复利用三角形法则和向量共线的概念，通过这题同学们应认识基底的作用.其实图中任何向量都可用e₁,e₂表示出来.

15．①②

③

（16）分析：如图：要证EFGH是平行四边形，只要证EH=FG且EH//FG.即证

解：如图E、F、G、H分别为AB、BC、CD、DA的中点，连BD，则

∴EFGH为平行四边形.

注：的含义是EH=FG且EH//FG.本　例的证法说明了向量是解决几何问题有力工具.