高中学生学科素质训练
高一数学同步测试(14)—数列的求和
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内.
1.设等差数列![]() 的前三项为5,
的前三项为5,![]() ,
,![]() ,其第
,其第![]() 项到第
项到第![]() 项的和为
项的和为![]() ,则当
,则当![]() 最小时
最小时![]() 应等于
( )
应等于
( )
A.6 B.5 C.4 D.3
2.数列![]() 中,a 1=-60,且a n+1 =an + 3,则这个数列的前30项的绝对值之和为( )
中,a 1=-60,且a n+1 =an + 3,则这个数列的前30项的绝对值之和为( )
A.495 B.765 C.3105 D.120
3.化简S n = n+(n-1)×2+(n-2)×2 2+……+2×2 n-2+2n-1的结果是 ( )
A.2 n+1+2-n-2 B.2n+1-n+2
C.2 n-n-2 D.2n+1-n-2
4、在项数为![]() 的等差数列中,所有奇数项和与偶数项和之比为
( )
的等差数列中,所有奇数项和与偶数项和之比为
( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
5.等比数列前![]() 项和为
项和为![]() ,已知
,已知![]() ( )
( )
A.28 B.256 C.512 D.1024
6.已知数列![]() 的前n项的和S n
= n 2-4n+1,则a 1+a 2+……+a 10的值是 ( )
的前n项的和S n
= n 2-4n+1,则a 1+a 2+……+a 10的值是 ( )
A.56 B.61 C.65 D.67
7.等比数列前![]() 项和为54,前
项和为54,前![]() 项和为60,则前
项和为60,则前![]() 项和为
(
)
项和为
(
)
A.66
B.64 C.![]() D.
D.![]()
8.己知等比数列![]() 的公比q<0,前n项的和Sn ,则S4 a5
与S5a4的大小关系为 ( )
的公比q<0,前n项的和Sn ,则S4 a5
与S5a4的大小关系为 ( )
A.S4a5 =S5 a4 B.S 4a5 >S 5a4
C.S4a5 <S5a4 D.不能确定
9.已知:Sn是等比数列![]() 的前n项和,S3,S9,S6成等差数列,则
的前n项和,S3,S9,S6成等差数列,则![]() ( )
( )
A.成等差数列 B.成等比数列
C.既成等差数列又成等比数列 D.既不成等差数列又不成等比数列
10.在50和350之间所有末位数是1的整数之和是 ( )
A.5880 B.5539 C.5208 D.4877
二、填空题:请把答案填在题中横线上.
11.一条信息,若一人得知后用一小时将信息传给两个人,这两个人又用一小时各传给未知此信息的另外两人,如此继续下去,一天时间可传遍 人.
12.一个有穷等比数列的首项为1,起奇数项的和为85,偶数项和为170,则该数列的公比为 ;项数为 .
13.在等比数列![]() 中
中![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() ;
;![]()
![]() .
.
14.设数列![]()
![]() ,则这个数列的前
,则这个数列的前![]() 项和为 .
项和为 .
三、解答题:解答应写出文字说明、证明过程或演算步骤.
15.设![]() 是等比数列,求证:
是等比数列,求证:![]() 成等比数列.
成等比数列.
16.数列{an}的前n项和![]() ,数列{bn}满足:
,数列{bn}满足:![]() .
.
(Ⅰ)证明数列{an}为等比数列;
(Ⅱ)求数列{bn}的前n项和Tn.
17.某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元,
(Ⅰ)问第几年开始获利?
(Ⅱ)若干年后,有两种处理方案:
(1)年平均获利最大时,以26万元出售该渔船;
(2)总纯收入获利最大时,以8万元出售该渔船.
问哪种方案合算.
18.已知数列![]() 中
中![]() 对于一切自然数
对于一切自然数![]() ,以
,以![]() 为系数的一元二次方程
为系数的一元二次方程![]() 都有实数根
都有实数根![]() 满足
满足![]() ,(1)求证:数列
,(1)求证:数列![]() 是等比数列;(2)求数列
是等比数列;(2)求数列![]() 的通项公式;(3)求
的通项公式;(3)求![]() 的前
的前![]() 项和
项和![]() .
.
19.已知数列![]() 的前n项和为
的前n项和为![]() .若a1=2,nan+1=Sn+n(n+1)
.若a1=2,nan+1=Sn+n(n+1)
(1)求数列![]() 的通项公式an
的通项公式an
(2)令![]()
①当n为何正整数值时,Tn![]() Tn+1
Tn+1
②若对一切正整数n,总有Tn≤m,求m的取值范围.
20.设数列![]() 的首项为
的首项为![]() 前n项和Sn满足关系式
前n项和Sn满足关系式![]() n=2,3,4,…)
n=2,3,4,…)
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比为
的公比为![]() ,作数列
,作数列![]() ,使得
,使得![]() ,求
,求![]() ;
;
(3)求和![]() .
.
高一数学(上)同步测试(14)参考答案
一、选择题:BBDAC DDBAA
9、解:∵S3,S9,S6成等差数列,∴S3+S6=2S9
若q=1,则S3=3![]() ,由
,由![]() ,与题设矛盾,
,与题设矛盾,![]()
![]()
整理,得q3+q6=2q9
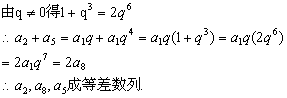
一、 填空题:
11、![]() ; 12、公比为2,项数为8; 13、
; 12、公比为2,项数为8; 13、![]() ,
,![]() 或
或![]() ;
;
14、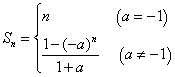
11、解:根据题意可知,获知此信息的人数成首项![]() 的等比数列,则一天内获知此信息的人数为:
的等比数列,则一天内获知此信息的人数为:![]() .
.
12、解:设此数列的公比为![]() ,项数为
,项数为![]() 项.由题意得:
项.由题意得: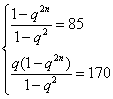
可得![]() ,
,![]() ,故此数列的公比为2,项数为8.
,故此数列的公比为2,项数为8.
13、解:∵![]() 是等比数列,∴
是等比数列,∴![]() , 又∵
, 又∵![]() ,
,
∴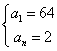 或
或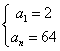 当
当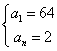 时
时![]() 得
得![]() ,∴
,∴![]() ;
;
当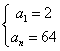 时
时![]() 得
得![]() , ∴
, ∴![]() .
.
14、解:∵![]() (与
(与![]() 无关的常数)
无关的常数)
∴该数列是等比数列,首项为1.当![]() 时,该数列的公比为1,则
时,该数列的公比为1,则![]() ;
;
当![]() 时,该数列的公比不为1,则
时,该数列的公比不为1,则![]() .
.
二、 解答题:
15、证明:设![]() 的公比为
的公比为![]() ,则
,则
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
![]() …
…![]()
∴![]() ,∴
,∴![]() 成等比数列.
成等比数列.
16、解:(Ⅰ)由![]() ,
,
两式相减得:![]()
![]() ,
,
![]() 同定义知
同定义知![]() 是首项为1,公比为2的等比数列.
是首项为1,公比为2的等比数列.
(Ⅱ)![]()
∴![]()
![]() 等式左、右两边分别相加得:
等式左、右两边分别相加得:
![]()
![]()
=![]()
17、解:(Ⅰ)由题设知每年费用是以12为首项,4为公差的等差数列,设纯收入与年数的关系为![]() ,∴
,∴![]() ,
,
获利即为![]() >0, ∴
>0, ∴![]() ,
,
解之得:![]() ,
,
又n∈N, ∴n=3,4,…,17, ∴当n=3时即第3年开始获利;
(Ⅱ)(1)年平均收入=![]()
∵![]() ≥
≥![]() ,当且仅当n=7时取“=”,
,当且仅当n=7时取“=”,
∴![]() ≤40-2×14=12(万元)即年平均收益,总收益为12×7+26=110万元,此时n=7.
≤40-2×14=12(万元)即年平均收益,总收益为12×7+26=110万元,此时n=7.
(2)![]() ,∴当
,∴当![]()
总收益为102+8=110万元,此时n=10,比较两种方案,总收益均为110万元,但第一种方案需7年,第二种方案需10年,故选择第一种.
18、解:(1)由题意得:![]() ,
,![]() ,代入
,代入![]() 得:
得:![]() ,当
,当![]() 时方程无实数根,∴
时方程无实数根,∴![]() ,
,
由等比数列的定义知:![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列;
的等比数列;
(2)由(1)知![]() , ∴
, ∴![]() ,
,
(3)![]()
![]()
![]() .
.
19、解:(1)∵nan+1=Sn+n(n+1),∴n=1时a2=2+2=4
n ≥2时nan+1 = Sn+n(n+1) ① (n-1)an = Sn-1+(n-1)n②
①- ②得 nan+1 -(n-1)an = an +2n, ∴n(an+1 - an)=2n
∴an+1 - an=2(n ≥2), 又a2-a1=2
∴数列{an}是首项为2,公差为2的等差数列,∴an=2n
(2)①∵Sn=![]() =n(n+1),∴Tn=
=n(n+1),∴Tn=![]()
令Tn![]() Tn+1, 即
Tn+1, 即![]() >
>![]() ,得n>2, 即n>2时Tn>Tn+1
,得n>2, 即n>2时Tn>Tn+1
②由①知当n>2时Tn>Tn+1 又T1=1<T2=3/2=T3
∴T2、 T3为{Tn}各项中数值最大的项,∴m≥T2=3/2
20、解:(1)∵3![]() ①
① ![]() ②
②
②—①得 ![]()
![]() ,∴
,∴![]() 是等比数列;
是等比数列;
(2)∵![]()
即 ![]() ;
;
(3)∵![]()
当n为偶数时,则![]()
![]()
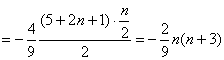 ;
;
当n为奇数时,则![]()
![]() .
.