高一数学下学期期末考试8
第Ⅰ卷（选择题 共60分）
参考公式：
三角函数积化和差公式 三角函数和差化积公式
sinαcosρ=
[sin(α+ρ)+sin(α﹣ρ)] sinα+sinρ=2sin
cos
cosαsinρ=[sin(α+ρ)﹣sin(α﹣ρ)] sinα﹣sinρ=2cossin
cosαcosρ=[cos(α+ρ)+cos(α﹣ρ)] cosα﹣cosρ=2coscos
sinαsinρ=－[cos(α+ρ)－sin(α﹣ρ)] cosα﹣cosρ=-2sinsin
y=Asinωx+Bcosωx=
sin(ωx+θ)，其中cosθ=
，sinθ=
θ∈
一、选择题（本大题共12小题，每题5分，共60分）
1．
用sin
，cos
，tan
，cot
，2sin
·cos作为集合A中的元素，则集合A中元素的个数为
A、2个 B、3个 C、4个 D、5个
2．已知点（3，4）在角α的终边上，则sinα+cosα+tanα的值为
A、
B、
C、
D、
3．已知a=8, b=6, 向量a、b所夹角为120°,则a﹣b为
A、2
B、
C、2
D、
4．已知集合M={aa=2kπ k∈z} P={aa=(2k+1)π k∈z)} Q={aa=(4k+1)π k∈z}
a∈M, b∈P 则a+b∈（ ）
A、M B、P C、Q D、不确定
5．若非零向量a、b，a不平行b,且a=b，那么向量a+b与a﹣b的关系是
A、相等 B、相交且不垂直 C、垂直 D、不确定
6．下列命题中正确的是
①a·b=ab ②(ab)2=a2·b2 ③a⊥(b－c)则ab－ac=0 ④a·b=0,则a+b=a－b
A、①② B、③④ C、①③ D、②④
7．在△ABC中，∠B为一内角，sinB－cosB>0, cotB<cosB, 则△ABC为
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形
8．下列不等式正确的是
A、sin<cos
B、sin≤cos C、sin>cos
D、sin≥cos
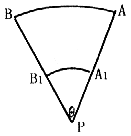9．如图扇形ABB1A1的中心角APB=θ，θ∈（0，2π），设PA1=x,
AA1=L, 给出下列四个结论①θ=
②AB<AB ③θ=
④S扇环ABB
A=
(L2+2Lx)其中正确的个数
A、1个
B、2个
C、3个
D、4个
10．有向线段
上有异于A、B的100个等分点P1P2……P100，则Pi(i=1、2、3…100)分有向线段的比λ的最大值与最小值分别为
A、101，
B、101，
C、100，
D、99，
11．若函数y=cos(2x－)+1的图像按
=(h·k), (h>0, 且h为最小角)平移后得到的图形是函数y=cos2x的图像，那么=（ ）
A、=（
，1） B、=（
，1） C、=（，-1） D、=（，-1）
12．已知cosα=
cos2α+cos2β，则sin2α+sin2β的范围为
A、[，+∞） B、[2，
]
C、[、]
D、[
，2]
第Ⅱ卷（非选择题 共90分）
二、填空题（本题共4小题，每题4分，共16分）
13．若sin2β=
，β为第二象限角，则tan2β=_________。
14．若
=（1，0），
=（1+
，1），
=（1，2），则△ABC的形状为______。
15．已知函数f(x)=x2，那么[f(a)+f(b)]与f(
)的大小关系为_______________，化简后为_____________。
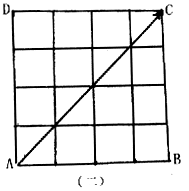
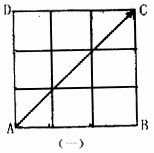
16．如图（一）边长为3的正方形中，有16个交点，从中任取2个组成向量，则与
平行且长度为2
的向量个数f(3)=8.
如图（二）边长为4的正方形中，有25个交点，从中任取2个组成的向量与向量平行且长度为3的向量个数f(4)=____________。
三、解答题（本大题共6小题，17题至21题每题12分，22题14分，共74分）
注意事项：要求写出必要的推理、证明、演算的过程。
17．（本题12分）已知在△ABC中，tanA=-
（1）求∠A （可用反三角表示）；
（2）求
的值。
18．（本题12分）如图：在直角坐标系中=a, =b，M为平面内的一点，M关于A的对称点S，S关于B的对称点为N。
（1）试用a,b表示向量
；
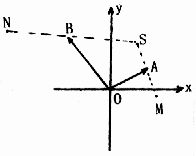（2）若A、B是动点，且=(cosα,sinα)， =(2cosβ,2sinβ)，求的取值范围。
19．（本题12分）若a、b、c∈R，且a=x2－2y+
,b=y2+,c=z2－2x+,求证：a、b、c中至少有一个大于零。
20．（本题12分）已知==1，，的夹角为120°。
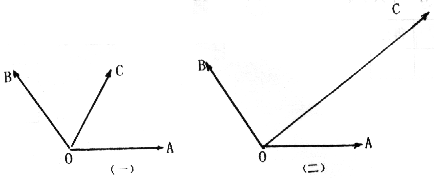
（1）若四边形OACB为平行四边表，试用、表示，并求；
（2）若=5，与的夹角为30°，试用，表示。
21．（本题12分）已知函数f(x)=Asinωx+Bcosωx,(A,B, ω∈R且ω>0)，若f(x)的最小正周期为1，且当x=
时f(x)取得最大值2。
（1）求f(x)的解析式；
（2）在[0，1）内求f(x)的单调区间，并说明单调性；
（3）在区间[
，3]上是否存在对称轴，若存在请求出对称轴方程，若不存在，请说明理由。
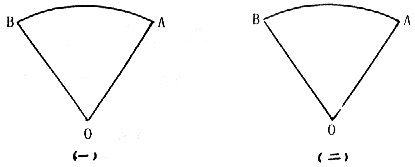
22．（本题满分14分）如图：扇形的半径为1，中心角为，请设计一种方案，使得扇形内接矩形的面积最大，求最大值，并说明理由。（内接矩形是指矩形的四个顶点都在扇形的弧上和半径上）
高一数学下学期期末考试8答案
一、选择题（本大题共12小题，每题5分，共60分）
1、C 2、D 3、A 4、B 5、C 6、B 7、C 8、A 9、D 10、C
11、D 12、D
二、填空题（本题共4小题，每题4分，共16分）
13、3
14、等边三角形（正三角形） 15、[f(a)+f(b)]≥f()
a2+b2≥2ab当且仅当a=b时取等号 16、f(4)=8
三、解答题（本大题共6小题，17至21题每题12分，22题14分，共74分）
17、解：（1）∵tanA=- ∴∠A为钝角
………………………………2分
即A=π－arctan
……………………………………5分
(2)
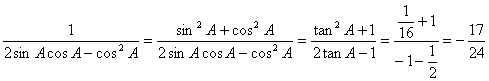…12分
18、解：（1）（法一）连接AB，得向量
=b－a
由三解形的中位线及平行向量得=2(b－a) （法二，可用坐标法） ……3分
（2）（法一）=2b－a,a－b≤b－a≤a+b
即∈[2，6]
（法二）=2
∵cos(α－β)≤1
∴2≤≤6
19、证明：设a≤0, b≤0, c≤0 ………………3分
则有a+b+c≤0
而a+b+c=(x2－2y+)+(y2－2z+)+(z2－2x+)
=(x－1)2+(y－1)2+(z－1)2+(π－3) ……………………8分
∵(x－1)2≥0 (y－1)2≥0 (z－1)2≥0 π－3>0 ……………………10分
∴a+b+c>0与a+b+c≤0矛盾
∴原命题正确 ……………………12分
20、解：（1）如图∵=，由向量的加法
法则得+=
……………………3分
∴=+，=
=1 …………5分
（2）如图，设=m+n，(m, n∈R)
∴≠0, ≠0
………………7分
∴·=m·+ n·
即 5×1×
=m－n
5×1×0=-
+n
m=
n=
∴=+
…………………12分
21、解：（1）f(x)=Sin(ωx+) Cosθ= Sinθ=
[θ∈[0,)
则ω=2π，=2，Sin（
+θ）=1，θ=
………………4分
∴f(x)=2Sin(2πx+)
（2）当2kπ－≤2πx+≤2π+，即k－
≤x≤k+ k∈z时增 …………5分
当2kπ+≤2πx+≤2π+π，即k+≤x≤k+
k∈z时减 …………6分
∵x∈[0,1) ∴在[0，]上增，[，]上减，[，1）上增 …………8分
（3）令2πx+= kπ+, x=
+
………………9分
即
≤
≤
k=5
………………11分
|
………………12分
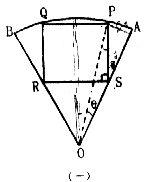22、解：如图（一）取AB上一点P，连OP，作矩形PQRS
设∠POA=θ(0<θ<)
………………1分
在△POS中，∠OSP=
PS=2Sinθ …………………2分
OS=2Sin(－θ)
在△OSR中
RS=OS ………………3分
S1=PS·RS=4Sinθ·Sin(－θ)
………………4分
=2[Cos(2θ－)－Cos]
≤2－
|
时取等号
………………6分（合计6分）
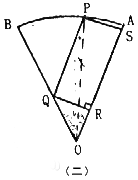如图（二）取AB上一点P，作矩形PQRS
设∠POA=θ，（0<θ<）
……………………1分
在△PSO中，PS=Sinθ
在△PQO中，∠POQ=－θ
∠PQO=
PQ=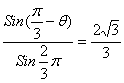
Sin(－θ)
S2=PQ·PS=
Sinθ·Sin(－θ)
=
[(Cos(2θ－)－Cos]
≤(1－)=
当θ=时取等号
…………………………6分（合计6分）
S1－S2=
<0
即S1<S2
∴如图二的矩形面积最大为
…………………………14分