高一数学月考试题
一、选择题（每小题4分，共64分）
1.下列说法中，正确的是（ ）
(A)数列1，2，3和数列3，2，1是同一数列
(B)数列1，2，3和数列1，2，3，4是同一数列
(C)数列1，2，3，4，…的一个通项公式是
(D)数列1，2，3，4，…的通项公式是
2.已知数列
的首项
，且
，则
的
值为（ ）
(A) 7 (B) 15 (C) 29 (D) 31
3.数列1，3，6，10，
，21，28…中的值为（
）
(A) 12 (B) 15 (C) 17 (D) 18
4.已知数列成等差数列，若
，则
的值为（ ）
(A) 12 (B) 13 (C) 14 (D) 16
5.设集合
，
，则
等于（
）
(A)
(B)
(C)
(D) 
6.函数
关于直线
对称的函数为（
）
(A)
(B)
(C)
(D)
7.函数
在
上为增函数，则
的取值范围是（
）
(A)
(B)
(C)
(D)
8.下列表示同一函数的是（ ）
(A)
(B)
(C)
(D)
9.函数
，则
的图象必过点（
）
(A) (0，1) (B) (1，1) (C)(
, 2） (D)
10.函数
的定义域为（
）
(A)
(B)
(C)
(D)
11.已知
( )
(A)
(B)
(C)
(D)
12.函数
的单调增区间是（ ）
(A)(1，+∞) (B)(-∞,0) (C)(-∞,1) (D)(0,+∞)
13.在国内投寄平信，每封信不超过20g，付邮资80分，超过20g而不超过40g，付邮资160分，依次类推，每封重g
的平信应付邮资为（单位：分）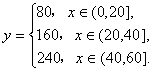
若某人投寄45g的平信，应付邮资（ ）
(A)80分 (B)160分 (C)240分 (D)320分
14.已知
，且
,则
( )
(A)-26 (B)-18 (C)-10 (D)10
15.函数
与直线的交点坐标为（ ）
(A)(0,0) (B)(0,0)，(1,1) (C)(-1,-1) ，(0,0) ，(1,1) (D)(-1,-1)
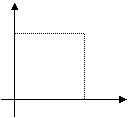
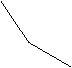
16.某学生离家去学校，为了锻炼身体，一开始匀速跑步前进，跑累了再匀速走余下的路程，下图中横轴表示出发后的时间
，纵轴表示离学校的距离
，则下列四个图中符合该学生的走法的是（ ）
 |  |  | |||||
 | |||||||
O
O
O
O
(A)
(B)
(C)
(D)
二、填空题（每小题4分，共24分）
17.函数
的定义域为
18.在等差数列中，若
19.在数列中，，
，则通项公式
20.函数
的定义域为
21.函数
，则
.
22.函数
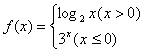,则
高一数学月考试题
班级 学号 姓名
一、选择题（每小题4分，共64分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 选项 |
二、填空题（每小题4分，共24分）
17. 18. 19.
20. 21. 22.
三、解答题（共66分，解答应写出文字说明，证明过程或演算步骤）
23.解不等式：（12分）
(1)
(2)
24.(12分)在等差数列中，已知
，求数列{
}的通项公式.
25. (12分)某商人如果将进货单价为8元/件的商品按10元/件出售时，每月可销售100件，已知商品每涨价1元/件，销售量就减少10件。问把销售价格定为多少时，才能赚取的利润最大,最大利润为多少元？
26. (12分)(1) 已知等差数列中，
，求
;
(2) 求数列
的前
项和 .
27. (14分)函数
(1)求证：
(2)画出函数
的图象；(3)由图象说出当为何值时，函数取得最小值?
附加题
28. （5分）定义在R上的函数满足关系式 
,
若数列满足
，求数列的前七项之和.
高一数学月考试题答案
一、选择题（每小题4分，共64分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 选项 | C | B | B | B | A | B | B | D | B | D | D | C | C | A | C | D |
二、填空题（每小题4分，共24分）
17.
18. 0 19.
20.
21. 0 22. 
三、解答题（共66分，解答应写出文字说明，证明过程或演算步骤）
23.解不等式：（12分）
(1) (2)
解：原不等式等价为 解：原不等式等价为
所以原不等式的解集为
原不等式的解集为
24.(12分)在等差数列中，已知，求数列{}的通项公式.
解：设数列的通项公式为
，则
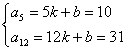
25. (12分)某商人如果将进货单价为8元/件的商品按10元/件出售时，每月可销售100件，已知商品每涨价1元/件，销售量就减少10件。问把销售价格定为多少时，才能赚取的利润最大,最大利润为多少元？
解：设此商品每月按10元/件的价格每件涨价元，则销售量减少10件，令赚取的利润为，于是
所以当
时，
360元，此时商品销售价格每件定为14元。
26. (12分)(1) 已知等差数列中，，求;
(2) 求数列的前项和 .
解：（1）由
得 (2) 由
得
100=2+2
27. (14分)函数 (1)求证：(2)画出函数的图象；(3)由图象说出当为何值时，函数取得最小值?
 |
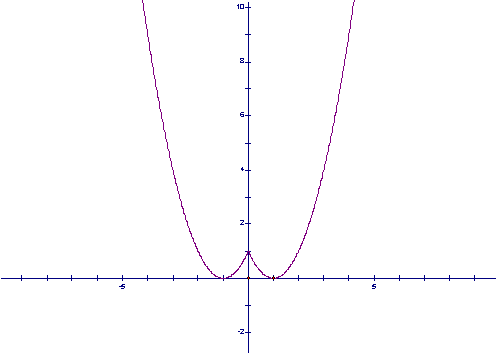
证明：(1)
(2)图象如上所示
（3）由图象知当
时，
.
28. （5分）定义在R上的函数满足关系式 ,
若数列满足，求数列的前七项之和.
解：由得
